|
GR0177 #45
|
|
|
|
|
Alternate Solutions |
ramparts
2009-10-07 14:30:21 | I made a stupid mistake as well (albeit not the same one as kev and f4hy, I actually squared the denonimators whle forgetting to square the numerators, lol), but I was able to guess the right answer using this reasoning:
The answer can be no more than 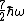 , so eliminate A, and (from the magnitudes of the coefficients) has to be greater than , so eliminate A, and (from the magnitudes of the coefficients) has to be greater than 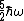 , so rule out C. D and E might be ruled out by those constraints, but more importantly, in a calculation like this there's no way you're going to get square roots in the denominator, you know the coefficients get squared. , so rule out C. D and E might be ruled out by those constraints, but more importantly, in a calculation like this there's no way you're going to get square roots in the denominator, you know the coefficients get squared.
So yes, requires some knowledge of quantum, but it works if you screw up the math ;) |  |
|
|
Comments |
ramparts
2009-10-07 14:30:21 | I made a stupid mistake as well (albeit not the same one as kev and f4hy, I actually squared the denonimators whle forgetting to square the numerators, lol), but I was able to guess the right answer using this reasoning:
The answer can be no more than 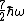 , so eliminate A, and (from the magnitudes of the coefficients) has to be greater than , so eliminate A, and (from the magnitudes of the coefficients) has to be greater than 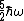 , so rule out C. D and E might be ruled out by those constraints, but more importantly, in a calculation like this there's no way you're going to get square roots in the denominator, you know the coefficients get squared. , so rule out C. D and E might be ruled out by those constraints, but more importantly, in a calculation like this there's no way you're going to get square roots in the denominator, you know the coefficients get squared.
So yes, requires some knowledge of quantum, but it works if you screw up the math ;) |  | kevglynn
2006-11-03 08:31:16 | Don't be stupid like I was when I took this test. I quickly did the calculation as you see above, then doing a little scan of the problem to make sure I hadn't missed anything, I saw the negative sign on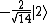 and decided to subtract that portion instead, thus switching from the correct answer to the incorrect answer. and decided to subtract that portion instead, thus switching from the correct answer to the incorrect answer.
f4hy
2009-04-02 16:37:12 |
I made the same mistake.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
