|
GR0177 #82
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Addition of Angular Momentum
For 2 electrons, one recalls that the there are three spin triplet states and one spin singlet state (hence their names). One can apply the lowering operator multiple times to the up-up state to arrive at, respectively, the up-down state, the down-up state, and then the down-down state (the spin-singlet state).
Applying the lowering operator to choice I, one gets choice III. Applying the lowering operator to that, one gets down-down. These are the 3 spin-triplet states.
By orthogonality, the down-down state has a negative sign. So, only choices I and III are in the triplet configuration.
(David J. Griffiths vanity alert---the QM problems thus far are all straight out of his textbook, An Introduction to Quantum Mechanics.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Walter
2008-12-28 14:52:36 | There are four possible spin states for the two electron system that are either symmetric or antisymmetric. There is only one that is antisymmetric, (hence singlet), but three that are symmetric, (hence triplet).
You need to be able to pick out the symmetric spin eigenfunctions. These will look the same after you exchange the labels for the electrons. This gives I and III.
Relabeling II makes it change sign - it's the antisymmetric singlet. |  | tensordyne
2008-10-31 14:49:35 | Answer is (C).
State I. has two electrons in the same state, ergo, it is out.
State II is antisymmetric and is therefore the singlet state of the two electrons, also out since the problem asks for a triplet state.
State III is symmetric and in a valid form to be a triplet.
Poop Loops
2008-11-01 21:09:52 |
Nope, the answer is D. It says so in my practice exam given by the ETS.
Where you went wrong is assuming that both spins up = same state. It is not. They can be in different orbital shells, but still have spin up.
|
| | StrangeQuark
2007-05-17 11:44:09 | Watch out don't be diss’n David!!! (Hint, Hint, Wink, Wink, that is because he was one of the author’s of the test’s, look at his E&M book and Elementary Particle book as well)
Shtego
2007-10-17 00:06:53 |
I'm weary of saying down-down is the condition for spin singlet state. One can derive the answer by applying the exchange operator and determining the sign of the eigenvalue. A +1 eigenvalue (of exchange operator) yields a symmetric state. A -1 value yields an anit-symmetic state. All symmetric states are grouped as a triplet and the anti-symmetric makes the singlet state. Explicitly:
Let X = exchange operator. A = up, B = down, and A1 = particle 1 up, B1 = particle 1 down, etc...
So, for choice I: X A1 A2 = A2A1 = (+1) A1A2
II: X(A1B2 - A2B1) = (A2B1 - A1B2) = (-1) (A1B2 - A2B1)
III: X (A1B2 + A2B1) = (+1) (A1B2 + A2B1)
So, only +1 eigenvalues are grouped in triplet state. (-1) is the singlet state.
|
gt2009
2009-06-10 22:02:21 |
Nope, 0 is the singlet state. You are writing spin states in the total spin basis, s=s1+s2. 2 spin 1/2 particles can only add up to total spin zero or 1 (given by CG coefficients), there is no -1.
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .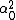
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
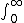| $\partial$ |
 |
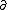| $\Rightarrow$ |
|
| $\ddot{x},\dot{x}$ |
 |
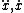| $\sqrt{z}$ |
 |
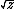| $\langle my \rangle$ |
 |
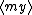| $\left( abacadabra \right)_{me}$ |
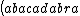_{me}) |
| $\vec{E}$ |
 |
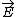| $\frac{a}{b}$ |
 |
|
|
|
|
|
