|
GR0177 #94
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Perturbation Theory }Perturbation Theory
The energy for first-order perturbation theory of 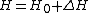 ( (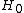 is the known Hamiltonian and is the known Hamiltonian and 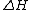 is the perturbed Hamiltonian) is given by is the perturbed Hamiltonian) is given by 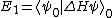 , where the wave-functions are the unperturbed ones. , where the wave-functions are the unperturbed ones.
Thus, the problem amounts to calculating ^2 | n \rangle) . This is just raising and lowering operator mechanics. . This is just raising and lowering operator mechanics.
^2=a^2+a^{\dag^2}+aa^\dag + a^\dag a) . But, after bra-ketting, one finds that the expectation value of . But, after bra-ketting, one finds that the expectation value of 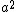 and and 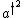 are 0, since are 0, since  and and 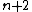 , ,  are orthogonal. Thus, the problem becomes, are orthogonal. Thus, the problem becomes,
 | n \rangle) . Applying the given eigen-equations, one finds that . Applying the given eigen-equations, one finds that  | n \rangle = (2n+1)V) . For . For 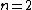 , one finds , one finds 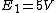 , as in choice (E). , as in choice (E).
(Note that: 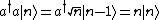 and and |n\rangle ) and and 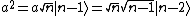 .) .)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
sjayne
2015-06-23 11:22:35 | I did it the same way. a ended up being 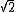 |1> and adagger was |1> and adagger was  |3> . Foiling it out any of the terms where |1> and |3> multiply go to 0, and in any of the terms where the kets are the same the kets go to 1. So you are left with V(2+3)=5V |3> . Foiling it out any of the terms where |1> and |3> multiply go to 0, and in any of the terms where the kets are the same the kets go to 1. So you are left with V(2+3)=5V |  | risyou
2012-11-07 22:49:18 | It just looks like the harmonic oscillator if you have tried to express them with the up down operator.
So I just put n=2 to it.. no answer so I give it up.
I feel so tried after doing 70+ question. |  | Donofnothing
2010-10-08 12:04:06 | this doesn't make much sense. I got the same answer from facotring out the (a+adagger) term, ignoring the (a*adagger), and using only a^2 and a^dagger squared. did i just get lucky, or is this alternate?
keradeek
2011-08-26 01:03:37 |
yeah, you just got super lucky.
|
FutureDrSteve
2011-11-04 17:34:55 |
Awesome! My plan is to get lucky on 100 problems in a row.... :S
|
yummyhat
2017-10-27 05:19:08 |
same\r\n
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
