|
GR8677 #12
|
|
|
|
|
Alternate Solutions |
flyboy621
2010-11-09 21:01:01 | I find it easier to look at the time between successive wave crests. Let's say if the source were at rest, the time between crests would be 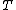 . Then if the source is moving toward the observer at . Then if the source is moving toward the observer at 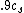 , the time between crests is , the time between crests is 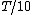 . Therefore the frequency is 10 times higher, as in (E). . Therefore the frequency is 10 times higher, as in (E). |  | kicksp
2007-10-29 10:11:11 | Quick hand-waving arguments save us time here. Note that the observed frequency 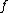 goes to infinity as goes to infinity as 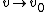 . A simple functional form for . A simple functional form for 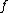 (which we could construct immediately even if we forgot the formula) is (which we could construct immediately even if we forgot the formula) is
}) , ,
yielding (E).
Go maroons! |  |
|
|
Comments |
ernest21
2019-08-10 03:09:24 | Just to be clear for people that might be foggy on vector calc, the answer is (A) for reasons already explained. techraptor |  | fredluis
2019-08-08 12:42:30 | I\'ve been browsing online more than three hours today, yet I never found any interesting article like yours. It is pretty worth enough for me. kitchen remodeling |  | fredluis
2019-08-08 12:38:28 | Just to be clear for people that might be foggy on vector calc, the answer is (A) for reasons already explained. bathroom remodel cost |  | joshuaprice153
2019-08-08 06:28:13 | enjoyed reading your articles. This is truly a great read for me. towing service |  | flyboy621
2010-11-09 21:01:01 | I find it easier to look at the time between successive wave crests. Let's say if the source were at rest, the time between crests would be 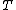 . Then if the source is moving toward the observer at . Then if the source is moving toward the observer at 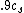 , the time between crests is , the time between crests is 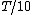 . Therefore the frequency is 10 times higher, as in (E). . Therefore the frequency is 10 times higher, as in (E). |  | student2008
2008-10-11 12:48:31 | ...the frequency of the wave is 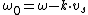 .... .... |  | student2008
2008-10-11 12:44:23 | The observable phase of the wave front at some point is 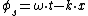 , where , where 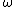 and and 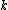 are the circular frequency and the wave vector measured in the observational reference frame. The source is moving with the constant velocity are the circular frequency and the wave vector measured in the observational reference frame. The source is moving with the constant velocity 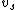 , so , so  . Thus, . Thus,  t) . It means that in the reference frame where the source is at rest the frequency of the wave is . It means that in the reference frame where the source is at rest the frequency of the wave is 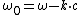 . Since . Since 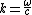 , we get eventually: , we get eventually: 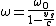 . . |  | ssp
2008-09-05 02:46:12 | Bit more handwaving...
So we take the fact that we know the frequency has to increase from above. Now we look at the speed. The shift has to large because the speed is large (speed and frequency are still proportional) and you got your answer, (E).
Little trick from GR |  | kicksp
2007-10-29 10:11:11 | Quick hand-waving arguments save us time here. Note that the observed frequency 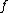 goes to infinity as goes to infinity as  . A simple functional form for . A simple functional form for  (which we could construct immediately even if we forgot the formula) is (which we could construct immediately even if we forgot the formula) is
}) , ,
yielding (E).
Go maroons!
vikhuan
2009-06-08 02:04:49 |
tyjyyty
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
