|
GR8677 #30
|
|
|
|
|
Alternate Solutions |
a_coiled_atom
2011-07-10 12:58:10 | Another way of thinking about it that might be helpful is that , in general, 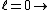 no orbital angular momentum no orbital angular momentum 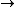 spherical symmetry. spherical symmetry. |  |
|
|
Comments |
joshuaprice153
2019-08-09 02:49:54 | Here has some effective and valuable information. Thanks for the information provided in this blog. This is the third time I visited in this blog. keep posting such stuff. Thanks a lot for the information. Randy Shine |  | a_coiled_atom
2011-07-10 12:58:10 | Another way of thinking about it that might be helpful is that , in general, 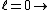 no orbital angular momentum no orbital angular momentum 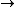 spherical symmetry. spherical symmetry. |  | suvas
2010-09-09 16:23:08 | I would choose E. The electronic charge distribution of atom is determined mainly by valence electron. |  | wittensdog
2009-07-25 17:54:02 | ETS is good at thinking of traps. I almost wanted to go for C. I saw the 4s1 electron being the least tightly bound, and in my mind a connection was made with the number 4. Clearly, l = 4 is supposed to trick you, when of course the electron actually has n = 4, not l = 4. It's value for orbital angular momentum is l = 0, of course.
jmason86
2009-08-16 16:36:12 |
I must have fallen for a trap too. I chose (A) immediately and without hesitation.
I was thinking that the n=3 shell only means the s-subshell. So when I saw that we were given 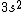 , I assumed that (A) was correct. However, the n=3 is a total shell consisting of the s, p, and d subshells... If (A) were true then we would be talking about Zinc with [Ar] , I assumed that (A) was correct. However, the n=3 is a total shell consisting of the s, p, and d subshells... If (A) were true then we would be talking about Zinc with [Ar] 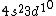 . .
|
neon37
2010-11-01 09:56:59 |
same here @ wittendog. Ofcourse reading E, changed made me realize my mistake.
|
|  | kyros
2007-10-30 21:42:24 | Shouldn't that be Sigma_4,0,0, since m can only range from -l to +l anyway? |  | simpsoxe
2006-11-30 21:20:14 | well the valence shell is 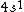 , but my question is about the other electrons in the lower shells. don't we have to consider them as part of the electron distribution? or do we assume they all have spherically symmetric distributions? (and why would that be?) , but my question is about the other electrons in the lower shells. don't we have to consider them as part of the electron distribution? or do we assume they all have spherically symmetric distributions? (and why would that be?)
Blake7
2007-07-23 18:26:38 |
The lower shells all appear to be completely filled
2 2 6 2 6
if I'm not mistaken that will make them all symmetric
|
kronotsky
2018-10-23 03:51:23 |
Filled subshells are the singlet component of the direct product of the component orbitals, so they have zero orbital angular momentum. So does 4s. The rotation operator(s) is an exponent of the orbital angular momentum operator, so it is equal to 1 (i.e. rotational symmetry).
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
