|
GR8677 #35
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
danielsw98667
2019-10-21 07:07:36 | I think the answer to this using the elastic potential energy. Hvac Tech Support
zachdun12493
2019-11-11 07:03:53 |
I agree with you. The answer is A. Jersey Watch
|
|  | joshuaprice153
2019-08-09 03:12:06 | Just wanted to say that I read your site quite frequently and I’m always amazed at some of the stuff people post. mobile window tinting |  | Almno10
2010-11-11 19:34:47 | I always think of that skater scott hamilton. He used to do back flips... had tons of energy. Hamiltonian is total energy.
Lagrangian on the other hand? Lagrange multipliers are for lazy people. Hard workers would optimize functions by guess and check (lazy = less energy T-V).
whatever.
mpdude8
2012-04-15 21:05:06 |
Hey, man, whatever works. I have some weird ways of remembering random crap too.
|
|  | a19grey2
2008-11-03 21:24:52 | Also, if you are unsure about the sign of the 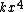 term you can just note that answer B) and D) are exactly equivalent through the relation noted by yosun in the original solution. Thus, ETS would never give TWO right answers and so the correct sign must be the unique answer given in A. term you can just note that answer B) and D) are exactly equivalent through the relation noted by yosun in the original solution. Thus, ETS would never give TWO right answers and so the correct sign must be the unique answer given in A.
BUT... you really should remember the sign conventions for the Hamiltonian and the Lagrangian.
BerkeleyEric
2010-01-12 21:48:15 |
Well, I suppose if they wanted to be really tricky they could have also had an option for (1/2)mv^2+ kx^4 to test if you know that Hamiltonians are in phase space (x, p_x) and Lagrangians are in state space (x, dx/dt).
|
neon37
2010-11-01 10:46:35 |
@BerkeleyEric - that is true but that wouldnt make either of them wrong.
Important thing is to remember that Hamiltonian is total energy of the system where as Lagrangian is not.
|
|  | Mexicorn
2005-11-08 12:11:38 | Like the last problem, the potential should be 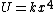
yosun
2005-11-09 02:24:56 |
Mexicorn: thanks for the typo-alert; it has been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 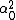 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
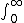 |
| $\partial$ |
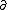 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
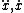 |
| $\sqrt{z}$ |
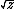 |
| $\langle my \rangle$ |
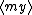 |
| $\left( abacadabra \right)_{me}$ |
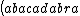_{me}) |
| $\vec{E}$ |
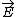 |
| $\frac{a}{b}$ |
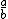 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
