|
GR8677 #37
|
|
|
|
|
Alternate Solutions |
lelandr
2011-04-24 12:37:38 | I think some users have already posted similar or close solutions, but not quite exactly this:
This problem definitely does not necessitate careful calculations, but rather just some dimensional analysis, limits, and a bit of common sense.
a) as 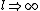 this solution approaches 0... qualitatively this is not correct, and (provided the mass of the rope is negligible) this should approach simply mg. this solution approaches 0... qualitatively this is not correct, and (provided the mass of the rope is negligible) this should approach simply mg.
b) 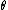 = 90 gives us 0... this clearly should not happen = 90 gives us 0... this clearly should not happen
c) wrong units... doesn't depend on g...
d) wrong units (w^2r^2 does not correspond to accelleration^2 as it should
e) units are correct, has correct limiting behavior at w,r=0, g= . this is our correct answer . this is our correct answer |  | nakib
2010-04-02 12:30:08 | T provides for both the circular motion and preventing the mass from falling towards earth. So one must expect two terms in the expression for T: one with an angular acceleration and the other with g. So, eliminate (A) and (B) and (C).
[One can also eliminate (A) and (B) by noting the directions they point at. (C) also has wrong units.]
(D) has wrong units. [centripetal acceleration is 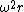 ] ]
(E) must be the answer. |  | spacebabe47
2007-09-30 08:36:46 | For some reason the concept of tension in force diagrams never made much sense to me.
A different way of looking at the problem. Think of the forces as making a right triangle. 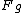 forms one leg pointing down, forms one leg pointing down, 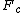 forms one leg pointing radially outwards, and forms one leg pointing radially outwards, and 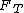 forms the hypotenuse along the string. forms the hypotenuse along the string.
Thus, 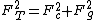
or 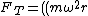^2+(mg)^2)^{1/2})
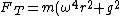^{1/2})
Answer E
|  | eshaghoulian
2007-09-15 05:14:12 | Can be done by limits/units: C/D have incorrect units; in the limit r = theta = 0, A gives you 0 tension (should be mg); B is maximized at theta=0 (gives mg) when, physically speaking, it should be minimized at that point (consider triangle inequality) |  |
|
|
Comments |
joshuaprice153
2019-08-09 03:20:29 | This post was very nicely written, and it also contains a lot of useful facts. I enjoyed your distinguished way of writing this post. pressure washing Orlando |  | mpdude8
2012-04-15 21:16:36 | There's a slew of problems with C -- not only units, but T = infinity if the angle is 0? No way.
In A, if r = 0 (i.e., mass is just hanging there), the tension does not = 0.
D is thrown out by units as well -- you can't add a squared acceleration (m^2 / s^4) to something with units (m^2 / s^2). One might be tempted to go with B, since at angle 0, T reduces to mg, but the tension should definitely not be 0 when the angle approaches 90 degrees. |  | lelandr
2011-04-24 12:37:38 | I think some users have already posted similar or close solutions, but not quite exactly this:
This problem definitely does not necessitate careful calculations, but rather just some dimensional analysis, limits, and a bit of common sense.
a) as 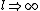 this solution approaches 0... qualitatively this is not correct, and (provided the mass of the rope is negligible) this should approach simply mg. this solution approaches 0... qualitatively this is not correct, and (provided the mass of the rope is negligible) this should approach simply mg.
b) 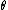 = 90 gives us 0... this clearly should not happen = 90 gives us 0... this clearly should not happen
c) wrong units... doesn't depend on g...
d) wrong units (w^2r^2 does not correspond to accelleration^2 as it should
e) units are correct, has correct limiting behavior at w,r=0, g=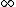 . this is our correct answer . this is our correct answer
OptimusPrime
2017-04-08 00:36:49 |
For (B), plugging in 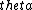 = 90 degrees gives 90/2 = 45 degrees. Then, cos(45) = = 90 degrees gives 90/2 = 45 degrees. Then, cos(45) = 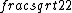 . It also has the correct dimensions. How else do we eliminate (B)? . It also has the correct dimensions. How else do we eliminate (B)?
|
|  | nakib
2010-04-02 12:30:08 | T provides for both the circular motion and preventing the mass from falling towards earth. So one must expect two terms in the expression for T: one with an angular acceleration and the other with g. So, eliminate (A) and (B) and (C).
[One can also eliminate (A) and (B) by noting the directions they point at. (C) also has wrong units.]
(D) has wrong units. [centripetal acceleration is 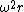 ] ]
(E) must be the answer.
flyboy621
2010-11-14 19:49:56 |
^ this
|
|  | BerkeleyEric
2010-01-12 22:13:16 | C and D have the wrong units, so those can be eliminated immediately. A fails to satisfy the limit of r=0. The expression for B in the limit of theta = pi (with the mass almost hitting the ceiling) gives zero tension, which does not make physical sense. So this leaves E. |  | spacebabe47
2007-09-30 08:36:46 | For some reason the concept of tension in force diagrams never made much sense to me.
A different way of looking at the problem. Think of the forces as making a right triangle. 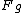 forms one leg pointing down, forms one leg pointing down, 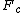 forms one leg pointing radially outwards, and forms one leg pointing radially outwards, and 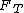 forms the hypotenuse along the string. forms the hypotenuse along the string.
Thus, 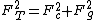
or 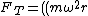^2+(mg)^2)^{1/2})
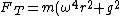^{1/2})
Answer E
wittensdog
2009-09-28 16:15:35 |
I think this is the fastest way to do this problem, and ETS loves to give useless information. The angle and length of the chord are totally unnecessary. I even hesitated for a minute on this one as a result of those pieces of information, from the power of suggestion throwing me off I suppose. But whenever you know the two perpendicular components of something, never even bother thinking about the angle. It's always true that,
T^2 = Tx^2 + Ty^2
where x and y are some perpendicular axes (in this case the vertical and radial directions are always perpendicular). The only time that angle information should even be considered is if you don't explicitly know Tx and Ty, or you're actually trying to find the angle, in which case, dividing the two expressions,
Tcos(theta/2) = mg,
Tsin(theta/2) = mrw^2
to give the tangent of theta/2 would definitely be the fastest, in my opinion. I personally think that trying to consider units in these problems is over-thinking everything way too much.
|
|  | eshaghoulian
2007-09-15 05:14:12 | Can be done by limits/units: C/D have incorrect units; in the limit r = theta = 0, A gives you 0 tension (should be mg); B is maximized at theta=0 (gives mg) when, physically speaking, it should be minimized at that point (consider triangle inequality) |  | shashiprakash
2007-07-26 00:11:40 | we can eliminate two answers on the basis of units. they are (C) and (D). |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
