GREPhysics.NET: GR8677 #4

GR8677 #4

Problem

GREPhysics.NET Official Solution

Wave Phenomena $\Rightarrow$ }Wave Equation

Perhaps this formula is more familiar: $y=A\sin(\omega t - k x)$ . But then again, they define the familiar quantities $k$ and $\omega$ for you in theirs...

(A) The amplitude is A. (Recall that the amplitude of $y=sin(x)$ is just 1, not 2.)

(B) How exactly does the argument of $\sin$ make it a traveling wave? Well, a traveling wave keeps the same waveform at all times. Thus, the overall argument has to be constant. $\omega t - kx = constant\Rightarrow x \propto - constant +\omega t$ . This looks like the old high school kinematics equation $x=-constant + vt$ . In fact, it's basically the same thing. That high school equation describes a particle going in the positive x-direction. So does this equation.

(C) Dimensions don't match. Period has units of time, not units of time/meter.

(D) The speed of the wave is $v=\lambda/T$ . From the kinematics explanation explained in (B), the velocity of the wave is obviously $v=\frac{\omega}{k}=\frac{2\pi\lambda}{2\pi T}$

(E) True. See (D) and (B).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

Prologue
2009-10-12 08:38:10

I think the explanation for B needs to be spelled out a little better. The wave looks the same in 'some reference frame traveling through space' no matter what time it is. This means you need to find a relationship between x and t such that the argument for sine gives a constant output through all time for the same x' - where x' is not the velocity but the space coordinate in the new moving frame. We need to find a 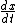$\frac{dx}{dt}$ such that $\frac{d[sin(x')]}{dt}=0$ . If you want this to be independent of time then that means the argument has to be constant with respect to time. So $2\pi(\frac{t}{T}-\frac{x}{\lambda})=constant=C$ . 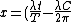Now you can solve for x to get $x=(\frac{\lambda t}{T}-\frac{\lambda C}{2 \pi})$ . 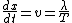Now you have the time dependence for x and you can just take the time derivative to get $\frac{dx}{dt}=v=\frac{\lambda}{T}$ .

I know this is long winded but these little details might be nice for someone that isn't comfortable with shifting.

Prologue
2009-10-12 10:54:45

That $\frac{d[sin(x')]}{dt}$ should logically be a $\frac{d[sin(\frac{2 \pi}{\lambda}x')]}{dt}$ but it doesn't change the rest of the post at all.

Reply to this comment

anmuhich
2009-03-19 08:39:59

Or you just know that for a sine wave the velocity is just the wavelength over the period.

Reply to this comment

icelevistus
2007-09-27 16:29:19

The only variables/constants we can assume the units of are x and t. All others are unspecified, despite what convention suggests.

Thus, the application of dimensional analysis for eliminating answers only works for D.

icelevistus
2007-09-27 16:30:20

Never mind, the units are implicit for the sin argument to be unitless.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone