|
GR9277 #10
|
|
|
Problem
|
|
\prob{10}
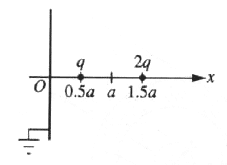
Two positive charges of q and 2q coulombs are located on the x-axis at x=0.5a and 1.5a, respectively, as shown above. There is an infinite, grounded conducting plane at x=0. What is the magnitude of the net force on the charge q?
-
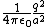
-
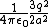
-
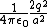
-
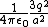
-
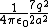
|
Electromagnetism }Image Charges }Image Charges
The conductor induces image charges -q and -2q since it is grounded at 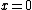 . Since these are (mirror) image charges, each charge induced is the same distance from the conducting plane as its positive component. . Since these are (mirror) image charges, each charge induced is the same distance from the conducting plane as its positive component.
The net force on q is just the magnitude sum of the positive charge 2q and the two induced charges, 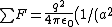 + 2/(2a^2) + 2/(a^2) \right) = \frac{q^2}{4\pi\epsilon_0a^2}\left( 1+1/2+2 \right) = \frac{q^2}{4\pi\epsilon_0a^2}\frac{7}{2}) , as in choice (E). , as in choice (E).
(Why is it the magnitude sum? Well, recall that 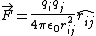 , where , where 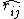 is the vector pointing from the charge one is interested in to the field charge, i.e., the other charge. If one has two positive charges, then the force points along that unit vector. However, if one has a minus charge and a positive charge, the force points in the other direction. Thus, all the force quantities are additive, and one might as well just take the magnitude sum.) is the vector pointing from the charge one is interested in to the field charge, i.e., the other charge. If one has two positive charges, then the force points along that unit vector. However, if one has a minus charge and a positive charge, the force points in the other direction. Thus, all the force quantities are additive, and one might as well just take the magnitude sum.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
memyselmineni
2014-11-19 10:58:10 | For grounded condoctor treat like mirror image!!!!!! Get help for such questions from http://www.amazon.com/Physics-Mathematica-Jude-Ndubuisi-Onicha/dp/1499691920/ref=sr_1_fkmr1_1?s=books&ie=UTF8&qid=1401627044&sr=1-1-fkmr1&keywords=physics+mathematica++2nd+edition+by+onicha+jude |  | antithesis
2007-10-05 17:41:25 | In the first equation, I believe the it should be ^2) in the second term, and not in the second term, and not 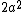 as it is right now. as it is right now.
nirav_605
2012-03-20 08:33:10 |
Agreed!
|
|  | timsaucer
2006-11-01 16:58:25 | If you look at it a little more rigorously, 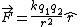 , where , where 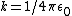 . Consider charge +q interacting with charge +2q. The direction of this force is pushing the +q charge to the left (similarly the +2q charge to the right). Now consider the image charges -q and -2q. Each of them have an attractive force on charge +q. This tends to move charge +q to the left as well. Since these forces are acting in the same direction, you add up their magnitudes. Mathematically: . Consider charge +q interacting with charge +2q. The direction of this force is pushing the +q charge to the left (similarly the +2q charge to the right). Now consider the image charges -q and -2q. Each of them have an attractive force on charge +q. This tends to move charge +q to the left as well. Since these forces are acting in the same direction, you add up their magnitudes. Mathematically:
![\vec{F}_{tot} = k q \left[ \frac{+2q}{a^2} (- \hat{x}) + \frac{-q}{a^2} ( \hat{x} ) + \frac{-2q}{(2a)^2} ( \hat{x} ) \right]](/cgi-bin/mimetex.cgi?\vec{F}_{tot} = k q \left[ \frac{+2q}{a^2} (- \hat{x}) + \frac{-q}{a^2} ( \hat{x} ) + \frac{-2q}{(2a)^2} ( \hat{x} ) \right])
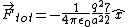
Rift
2011-02-28 16:53:23 |
Why is the direction of the -q and -2q equal to  and not - and not - ? I understand that the forces add up from drawing out the Forces... but mathematically my magnitude sum is not as I expected it to be since i used - ? I understand that the forces add up from drawing out the Forces... but mathematically my magnitude sum is not as I expected it to be since i used -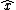 as the direction of the force on q for -q and -2q. as the direction of the force on q for -q and -2q.
|
Rift
2011-02-28 18:23:11 |
disregard previous comment. I know what I did. Thanks!
|
|  | blackholepioneer
2006-10-29 23:45:29 | one thing i don\'t understand is, why do the forces add? Shouldn\'t the force between q and 2q have an opposite sign compared to the force between -q and q, and -2q and q, in that case, when you add them up, you get q^2/2a, which isn\'t one of the choices. I\'d appreciate it if someone can clarify this for me.
gray
2007-10-03 06:35:40 |
They're all in the same direction because the force from the positive charge on the right is repulsive (and therefore to the left), and the forces from the negative charges on the left are attractive (and therefore also to the left).
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 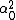 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
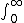 |
| $\partial$ |
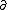 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
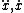 |
| $\sqrt{z}$ |
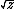 |
| $\langle my \rangle$ |
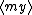 |
| $\left( abacadabra \right)_{me}$ |
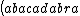_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
