|
GR9277 #23
|
|
|
|
|
Alternate Solutions |
claire
2009-09-12 11:31:59 | If you don't want to have to bother with the big numbers for the approximation, you can use your knowledge that for room temperature (~300K) you have kT=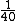 eV (this is a useful thing to know). And you know that an electron mass is .5MeV/c eV (this is a useful thing to know). And you know that an electron mass is .5MeV/c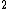 . .
The problem uses 80,000K, but do it for 90,000, since thats easier with the numbers you know.
Then kT~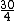 , so , so  = =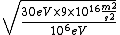 ~ ~ 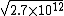 ~ 2 ~ 2  10 10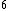 m/s, option (E). m/s, option (E). |  |
|
|
Comments |
rwmurphy
2012-11-08 12:58:40 | I have a slight issue with the wording of this problem: it only states that the Fermi temperature of copper is at 80000K, not that the copper is actually at the fermi temperature. I mistakenly thought the ETS was just trying to be tricky and asking for a reasonable drift velocity in Cu, which then (A) would be the answer.
*sigh*
When I look at it now, it easy to assume that they mean copper is at that temperature, but under a crunch for time, your brain does funny things! Either way, they should make it less ambiguous.
NSF Fellow
2013-09-18 11:13:11 |
It says conducting electrons! they are at fermi energy!
|
NoPhysicist3
2017-03-23 09:38:59 |
same sh*t man
|
NoPhysicist3
2017-03-23 09:42:00 |
but as i noticed GRE problems tend to use all information given in the task
|
|  | Quark
2011-10-25 14:35:18 | Why do we use kT for the energy and not 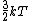 for the three translational degrees of freedom in finding the kinetic energy? for the three translational degrees of freedom in finding the kinetic energy?
liliapunto
2013-07-14 03:15:52 |
This is exactly what I did and what I want to ask about.
|
Prufrock
2013-09-03 15:04:01 |
Because condensed matter physicists don't recognize factors as small as 3/2 - and in this problem it is certainly true that the 3/2 is insignificant.
|
NSF Fellow
2013-09-18 11:14:37 |
it's not a gas!
|
NSF Fellow
2013-09-18 13:08:25 |
and it says the Fermi temperature of Cu, not the temperature Cu is at.
|
|  | neon37
2010-11-11 03:59:18 | Here we can clearly get away with order of magnitude approximation, so dont bother about any numbers except 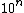 ones. You will get the answer in less than a minute. ones. You will get the answer in less than a minute. |  | nyuko
2009-10-30 10:10:08 | I did this problem in seconds. I just remember the typical Fermi speed for electron in metals is of the order 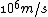
I think there are some typical values for physicists to remember. Fermi speed of electrons in metal is one. |  | claire
2009-09-12 11:31:59 | If you don't want to have to bother with the big numbers for the approximation, you can use your knowledge that for room temperature (~300K) you have kT=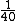 eV (this is a useful thing to know). And you know that an electron mass is .5MeV/c eV (this is a useful thing to know). And you know that an electron mass is .5MeV/c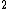 . .
The problem uses 80,000K, but do it for 90,000, since thats easier with the numbers you know.
Then kT~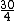 , so , so 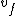 = =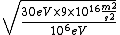 ~ ~ 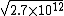 ~ 2 ~ 2  10 10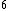 m/s, option (E). m/s, option (E). |  | ramparts
2009-08-02 17:36:13 | I did this much more quickly by just looking at orders of magnitudes. Ignoring dimensionless constants (which will never change the answer by a factor of 2), temperature depends on the energy divided by the Boltzmann constant, and the energy is roughly kinetic energy, mv^2. So we have
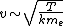
Plug in the appropriate factors of 10, and you get 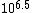 . Excellent. . Excellent.
I have no idea if the physics is right, but the dimensions work out and the answer is right ;)
Albert
2009-11-03 05:05:17 |
Yes, your method is really bad. Not only your physics is abominable, your math is plain wrong too. You got the formula wrong and that's besides the fact that you did basically the same thing as Yosun, just didn't write the steps. And then got it all mixed up. I wonder how you ever reached the answer (or did you?). Sorry, but it's important that truth be spoken.
|
Ryry013
2019-10-17 10:04:21 |
This gives an answer around 10^29 I believe, definitely wrong (;・﹏・)
|
|  | none
2008-10-19 23:01:52 | If you write things a bit differently you get 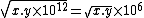 . The only answer with the right order of magnitude is (E) . The only answer with the right order of magnitude is (E) |  | student2008
2008-10-14 09:58:44 | Actually, ETS means the average velocity modulus, 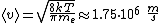 , which can be obtained using the Maxwell distribution. Though such rigorous formula isn't relevant for the real exam, of course. , which can be obtained using the Maxwell distribution. Though such rigorous formula isn't relevant for the real exam, of course.
student2008
2008-10-14 10:08:31 |
Even more precise would be 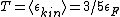 and and 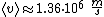 , but apparantely it's not for the exam :) , but apparantely it's not for the exam :)
|
student2008
2008-10-15 00:14:53 |
Stupid me, all I wrote above is wrong. In fact, the concept of Fermi-gas (and Fermi-energy) of electrons requires 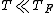 , not , not 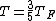 . What is relevant here is the low-temperature Fermi distribution of electrons . What is relevant here is the low-temperature Fermi distribution of electrons \simeq\theta(p_F - p)) (which is true up to melting temperatures: (which is true up to melting temperatures: 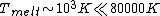 ), not the Maxwell distribution. However, the problem asks about the mean speed of the ), not the Maxwell distribution. However, the problem asks about the mean speed of the  electrons. And these are the electrons near the Fermi surface, since only their energy may change (under the not-extremely-high voltage). So, Yosun's solution is right, with this reservation. electrons. And these are the electrons near the Fermi surface, since only their energy may change (under the not-extremely-high voltage). So, Yosun's solution is right, with this reservation.
|
|  | prismofmoonlight
2007-10-31 11:22:40 | I think T_F is 8E4, not 8E5 as given in your equation (though the change is not enough to affect the approximation too terribly much).
Thanks for the great site! |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
