|
GR9277 #33
|
|
|
|
|
Alternate Solutions |
kap09c
2013-10-17 15:11:53 | This was my 30 second method: Whenever resistors are in parallel, the equivalent resistor will always be lower than the smallest value. It is easy to see the max total resistance is 50+50=100 ohm. Therefore the max current of the entire circuit is 3/(100) = .03 A.
Now take this and evaluate using the max resistance of the section under question, which would be 30 ohm. The max value for the voltage there is then 0.9 V. This eliminates everything but A and B. Realizing you took two maximizing approximations, opt for the lesser of the two, which is A.
BOOM SHAKALAKA! |  | gravity
2010-11-08 00:39:11 | This problem (like all PGRE problems) is not as hard or tedious as it seems.
This equation will save your life one day, for two resistors in parallel:
R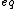 = R = R *R *R / (R / (R + R + R ) )
(same form for capacitors in parallel). Memorize it.
Using this, you should be able to break down all the resistors to one R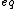 = 75 = 75 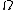 in about 5 seconds. And you now know current is 1/25. in about 5 seconds. And you now know current is 1/25.
Quickly solve the voltage drop across the first resistor like everybody else says. Or don't. I don't care.
Note that the equivalent resistance R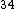 = 6*3/(6+3) = 20 and adding 30 for R = 6*3/(6+3) = 20 and adding 30 for R is 50. It's the equivalent of two resistors of the same resistance! Thus, the current is split evenly between the two. 1/25 becomes 1/50 (Amps). The equivalent resistance is 20 (Ohms) and you know the same voltage drops across parallel resistors. is 50. It's the equivalent of two resistors of the same resistance! Thus, the current is split evenly between the two. 1/25 becomes 1/50 (Amps). The equivalent resistance is 20 (Ohms) and you know the same voltage drops across parallel resistors.
20/50 = .4
There, didn't take long at all, and now you have free time to doodle or something.
Tsaigos
2014-03-29 20:31:49 |
If you really wanted to expand it all it is for multiple parallel resistors is
_{parallel}) = = 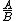
where A is Π_{n})
and B is Σ (Π _{n}) _{i-}) ) )
where _{i-}) represents i removed represents i removed
|
|  | his dudeness
2010-10-09 07:24:55 | In problems like these, if you do the full calculation, then you play right into ETS's hands -- it ends up taking 3-5 minutes and the terrorists win.
A quicker way is as follows:
(1) Quickly calculate the equivalent resistance of the circuit to be 75 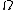 (this shouldn't take more than about a minute). This means the total current is (this shouldn't take more than about a minute). This means the total current is 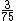 A. A.
(2) Note that if the full current would be flowing through our resistor 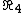 , then the voltage would be , then the voltage would be 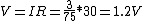 . Thus we can immediately eliminate D and E. . Thus we can immediately eliminate D and E.
(3) However, the actual current flowing through R4 is less than half the total current, so V < 0.6 and choice A is the only one that fits the bill.
Of course, when I actually solved the problem I did it the long-winded way, but in hindsight this is how I would have approached it. |  | niux
2009-11-06 13:14:30 | You can do it in 4 quick mental steps (and save time)
As from previous question you got equivalent resistances, then I better used voltage because it divides proportional to resistance when they are in series. You start with 3V from the battery, so here it goes:
1)3 V  2V to R1 and 1V to 2V to R1 and 1V to  (=R2,3,4,5) because they are in series (=R2,3,4,5) because they are in series
2)1V to R2 and 1V to the other branch R3,4,5 (parallel)
3)0.4V to R3,4 and 0.6V to R5
4) 0.4 V to R4 (parallel with R3 so same voltage)
Although you may be tempted to skip it, this circuit is not that much complicated, so you can try. |  | jmason86
2009-09-04 19:27:13 | My user solution for this problem is..
SKIP IT.
Long resistance calculations like this take a long time to do, require many small steps, which increases the likelihood that you will make some small mistake and totally botch the answer (as is evidenced by multiple typos in Yosun's solution and even in the comments). They are unlikely to give you more than 2 problems of this type in the whole test and the time would be MUCH better spent on other problems, or returning to other, less mathematically intense problems. |  | qu
2008-10-13 07:24:52 | R1, R2 and R5 are in series just ignoring the R3 and R4 parallel block. Equivalent (R1,R2,R5) is 130 ohm. Current through them is i=v(3)/Req(130)=0.02. Now the parallel block has equivalent rsistance as Req1=(1/R3+1/R4)^-1. Voltage drop across parallel bloc is therefore V=i*Req1(20ohm); which is 0.4 approx. so choice is (A) |  | chrisfizzix
2008-10-06 12:11:04 | I hate all those annoying reciprocal relations. Here's a way to solve the problem while doing as little annoying circuit manipulations as possible, and instead using some simple relations.
Find the equivalent resistance of 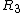 || ||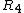 : : 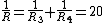 ohms. ohms.
So, the total resistance of the right branch is 20 + 30 = 50 ohms.
Find the equivalent resistance of the whole circuit: this is straightforward if you remember that two equal resistors in parallel give you one resistor of half the value. So, our total resistance is 75 ohms.
Find the current: 3.0 volts / 75 ohms = 1/25 amps.
Find the voltage drop across 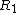 : this is easy: : this is easy: 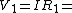 2.0 V. 2.0 V.
Now we know that the voltage across the right branch is 1.0 V, and that half the total current is flowing through the branch as the resistance of the middle and right branches are equal.
The voltage drop across 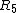 is is  V. So, we know the voltage drop over the top portion of the right branch: 1.0 V - 0.6 V = 0.4V, choice A. V. So, we know the voltage drop over the top portion of the right branch: 1.0 V - 0.6 V = 0.4V, choice A. |  |
|
|
Comments |
philip_kent
2017-10-19 04:54:22 | The equivalent resistance for the three resistors on the far right is 60*30/90=20 + 30 = 50 which in parallel with the other 50 ohm resistor gives a total equivalent resistance of 50/2 for the right side, which is half the top resistance. So you now only have two resistors, 50 and 50/2, with the same current running through them. Since P = 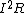 the top resistor must dissipate more energy than the rest of the circuit since it\'s resistance is twice as big. All the resistors on the right share a portion of half that energy so they must all be less than the power dissipated by R1, and the choice is A. the top resistor must dissipate more energy than the rest of the circuit since it\'s resistance is twice as big. All the resistors on the right share a portion of half that energy so they must all be less than the power dissipated by R1, and the choice is A. |  | kap09c
2013-10-17 15:11:53 | This was my 30 second method: Whenever resistors are in parallel, the equivalent resistor will always be lower than the smallest value. It is easy to see the max total resistance is 50+50=100 ohm. Therefore the max current of the entire circuit is 3/(100) = .03 A.
Now take this and evaluate using the max resistance of the section under question, which would be 30 ohm. The max value for the voltage there is then 0.9 V. This eliminates everything but A and B. Realizing you took two maximizing approximations, opt for the lesser of the two, which is A.
BOOM SHAKALAKA! |  | kap09c
2013-10-17 14:48:58 | This was my 30 second method: Whenever resistors are in parallel, the equivalent resistor will always be lower than the smallest value. It is easy to see the max total resistance is 50+50=100 ohm. Therefore the max current of the entire circuit is 3/(100) = .03 A.
Now take this and evaluate using the max resistance of the section under question, which would be 30 ohm. The max value for the voltage there is then 0.9 V. This eliminates everything but A and B. Realizing you took too maximizing approximations, opt for the less of the two, which is A.
BOOM SHAKALAKA!
kap09c
2013-10-17 14:49:51 |
two* ... sorry. need more coffee.
|
|  | walczyk
2011-03-26 04:27:38 | easiest with lenz' law... |  | gravity
2010-11-08 00:39:11 | This problem (like all PGRE problems) is not as hard or tedious as it seems.
This equation will save your life one day, for two resistors in parallel:
R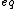 = R = R *R *R / (R / (R + R + R ) )
(same form for capacitors in parallel). Memorize it.
Using this, you should be able to break down all the resistors to one R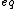 = 75 = 75 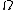 in about 5 seconds. And you now know current is 1/25. in about 5 seconds. And you now know current is 1/25.
Quickly solve the voltage drop across the first resistor like everybody else says. Or don't. I don't care.
Note that the equivalent resistance R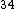 = 6*3/(6+3) = 20 and adding 30 for R = 6*3/(6+3) = 20 and adding 30 for R is 50. It's the equivalent of two resistors of the same resistance! Thus, the current is split evenly between the two. 1/25 becomes 1/50 (Amps). The equivalent resistance is 20 (Ohms) and you know the same voltage drops across parallel resistors. is 50. It's the equivalent of two resistors of the same resistance! Thus, the current is split evenly between the two. 1/25 becomes 1/50 (Amps). The equivalent resistance is 20 (Ohms) and you know the same voltage drops across parallel resistors.
20/50 = .4
There, didn't take long at all, and now you have free time to doodle or something.
gravity
2010-11-08 00:40:37 |
Capacitors in series! In series, I mean!
*Don't blame me for when you fail. You're the failure.
|
Kabuto Yakushi
2010-11-12 15:04:02 |
You beat me to it by ten seconds. LOL.
|
laxatives
2012-08-07 13:37:50 |
I think you meant same form for capacitors in series
|
laxatives
2012-08-07 13:38:44 |
Damn, beat me to it by 2 years... Sorry I didnt see the comments in the alternate solutions section
|
godtripp
2012-10-03 22:25:48 |
I've always found it easier to remmemberrn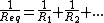 rnrnThis way you can easily add up all capacitors or resistors at once no sweat.rn rnrnThis way you can easily add up all capacitors or resistors at once no sweat.rn
|
Tsaigos
2014-03-29 20:31:49 |
If you really wanted to expand it all it is for multiple parallel resistors is
_{parallel}) = = 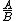
where A is Π_{n})
and B is Σ (Π _{n}) _{i-}) ) )
where _{i-}) represents i removed represents i removed
|
NoPhysicist3
2017-03-23 10:16:50 |
Capacitors in series, the same as resistors in parallel
|
|  | his dudeness
2010-10-09 07:24:55 | In problems like these, if you do the full calculation, then you play right into ETS's hands -- it ends up taking 3-5 minutes and the terrorists win.
A quicker way is as follows:
(1) Quickly calculate the equivalent resistance of the circuit to be 75 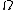 (this shouldn't take more than about a minute). This means the total current is (this shouldn't take more than about a minute). This means the total current is 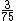 A. A.
(2) Note that if the full current would be flowing through our resistor 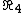 , then the voltage would be , then the voltage would be 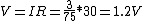 . Thus we can immediately eliminate D and E. . Thus we can immediately eliminate D and E.
(3) However, the actual current flowing through R4 is less than half the total current, so V < 0.6 and choice A is the only one that fits the bill.
Of course, when I actually solved the problem I did it the long-winded way, but in hindsight this is how I would have approached it.
worseredgirl
2011-10-12 18:50:42 |
This is the best answer, aside from skipping the problem all together (which is what I did)
|
|  | niux
2009-11-06 13:14:30 | You can do it in 4 quick mental steps (and save time)
As from previous question you got equivalent resistances, then I better used voltage because it divides proportional to resistance when they are in series. You start with 3V from the battery, so here it goes:
1)3 V  2V to R1 and 1V to 2V to R1 and 1V to  (=R2,3,4,5) because they are in series (=R2,3,4,5) because they are in series
2)1V to R2 and 1V to the other branch R3,4,5 (parallel)
3)0.4V to R3,4 and 0.6V to R5
4) 0.4 V to R4 (parallel with R3 so same voltage)
Although you may be tempted to skip it, this circuit is not that much complicated, so you can try.
NoPhysicist3
2017-03-23 10:25:19 |
Amazing solution
|
|  | jmason86
2009-09-04 19:27:13 | My user solution for this problem is..
SKIP IT.
Long resistance calculations like this take a long time to do, require many small steps, which increases the likelihood that you will make some small mistake and totally botch the answer (as is evidenced by multiple typos in Yosun's solution and even in the comments). They are unlikely to give you more than 2 problems of this type in the whole test and the time would be MUCH better spent on other problems, or returning to other, less mathematically intense problems.
apr2010
2010-04-07 16:44:28 |
I have written down the formula and concluded the same. As question 32 is pretty simple, you got already point for that.
|
|  | infiniteseries
2008-10-29 19:37:59 | there seems to be an error with this image. Just a heads up. |  | qu
2008-10-13 07:24:52 | R1, R2 and R5 are in series just ignoring the R3 and R4 parallel block. Equivalent (R1,R2,R5) is 130 ohm. Current through them is i=v(3)/Req(130)=0.02. Now the parallel block has equivalent rsistance as Req1=(1/R3+1/R4)^-1. Voltage drop across parallel bloc is therefore V=i*Req1(20ohm); which is 0.4 approx. so choice is (A)
ramparts
2009-08-15 18:32:56 |
How are those three in series? R2 and R5 seem pretty clearly parallel to me...
|
|  | qu
2008-10-13 07:23:55 | R1, R2 and R5 are in series just ignoring the R3 and R4 parallel block. Equivalent (R1,R2,R5) is 130 ohm. Current through them is i=v(3)/Req(130)=0.02. Now the parallel block has equivalent rsistance as Req1=(1/R3+1/R4)^-1. Voltage drop across parallel bloc is therefore V=i*Req1(20ohm); which is 0.4 approx. so choice is (A) |  | chrisfizzix
2008-10-06 12:11:04 | I hate all those annoying reciprocal relations. Here's a way to solve the problem while doing as little annoying circuit manipulations as possible, and instead using some simple relations.
Find the equivalent resistance of 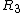 || ||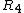 : : 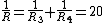 ohms. ohms.
So, the total resistance of the right branch is 20 + 30 = 50 ohms.
Find the equivalent resistance of the whole circuit: this is straightforward if you remember that two equal resistors in parallel give you one resistor of half the value. So, our total resistance is 75 ohms.
Find the current: 3.0 volts / 75 ohms = 1/25 amps.
Find the voltage drop across 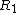 : this is easy: : this is easy: 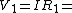 2.0 V. 2.0 V.
Now we know that the voltage across the right branch is 1.0 V, and that half the total current is flowing through the branch as the resistance of the middle and right branches are equal.
The voltage drop across 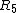 is is  V. So, we know the voltage drop over the top portion of the right branch: 1.0 V - 0.6 V = 0.4V, choice A. V. So, we know the voltage drop over the top portion of the right branch: 1.0 V - 0.6 V = 0.4V, choice A. |  | energy69
2007-10-14 20:39:53 | solution is so much more complicated then it needs to be. \...
sawtooth
2007-11-02 13:35:32 |
Indeed it is. Btw, doesn't "voltage across" mean the voltage drop?Anyway. Since one has found that the current going through 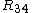 is 1/50 A just multiply by is 1/50 A just multiply by ![R_{34}=R_3 // R_4=20]Omega](/cgi-bin/mimetex.cgi?R_{34}=R_3 // R_4=20]Omega) to find a 0.6V drop (the same in both resistors. You can find the two respective currents and apply for to find a 0.6V drop (the same in both resistors. You can find the two respective currents and apply for 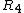 if you dont believe, but in the end you are using the fact that the voltage drop is the same. I dont know why the official solution uses if you dont believe, but in the end you are using the fact that the voltage drop is the same. I dont know why the official solution uses 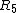 . .
|
|  | ec2250
2007-08-27 11:05:05 | I don't understand why the current across R2 is I. Wouldn't the current have split from I1 to I2 and I3 when the initial current reached the first junction? To clarify, I'm confused at the part where we find the voltage across R2. According to the loop rule, wouldn't it be V - I1R1 - I2R2 = 0?
D8less
2007-10-05 21:27:15 |
You are right. The author of the above answer mistyped it. The second comment from the bottom mentions there is an error in the result that V2=2 using i1=i2. The correct correction is that i1=2i1 as you said.
|
|  | hamood
2007-04-02 13:29:37 | combined resistance of R3 and R4 is 20. So both the right arm and the middle arm have the same resistance of 50 ohms. Half the current goes through each, meaning I = 3/150. So drop across R4= drop across R3= IR = 3/150 * 20 = 0.4 V |  | bterranova
2006-11-02 09:49:28 | typo on the typo
R34^-1=1/20 | 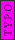 | bterranova
2006-11-02 09:46:07 | Another typo:
R34^-1=(1/30+1/60)^-1 |  | comorado
2006-10-26 01:23:22 | Another mistyp:  instead of instead of  |  | comorado
2006-10-26 01:13:28 | Must be 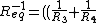^{-1}+R_5)^{-1}+\frac{1}{R_2})
Instead of 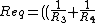^{-1}+R_5)^{-1}+\frac{1}{R_2}) |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
