|
GR9277 #62
|
|
|
|
|
Alternate Solutions |
djh101
2014-09-02 13:56:24 | Solution by elimination:
-Eliminate A immediately because change in volume requires work to be done.
-Work should be positive when volume increases, negative when volume decreases, and 0 when there is no change. Eliminate B.
-The process is reversible, so switching V1 and V0 should give an answer with the same magnitude but opposite sign. This only leaves E. You could actually eliminate all but E with this step alone. |  |
|
|
Comments |
djh101
2014-09-02 13:56:24 | Solution by elimination:
-Eliminate A immediately because change in volume requires work to be done.
-Work should be positive when volume increases, negative when volume decreases, and 0 when there is no change. Eliminate B.
-The process is reversible, so switching V1 and V0 should give an answer with the same magnitude but opposite sign. This only leaves E. You could actually eliminate all but E with this step alone. |  | greatspirits
2012-11-01 15:56:50 | I was actually way too zombified from studying by the time I got to this problem, I couldn't even think, usually this would be easy for me, but since I had done the work before, I just remembered that there was a 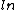 in the expression, so E. in the expression, so E.
|  | bkardon
2007-10-05 11:00:46 | Wait - so the information about 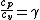 was a total red herring? was a total red herring?
ewhite2
2007-10-27 12:50:31 |
yup
|
FortranMan
2008-10-01 19:23:02 |
they're trying to confuse you into thinking that the adiabatic exponent or the compression ratio is involved, when both really aren't since neither gamma is defined with the specific heats. And considering gamma is normally used as an exponent, why would you divide the specific heats anyway?
|
Nathan_Grey
2010-01-31 22:30:13 |
FortranMan: I understand that gamma is not needed for this problem, but gamma is customarily the variable used to define the ratio of specific heats. It is also related to the degrees of freedom by: 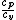 =gamma= =gamma=)
|
kaic
2013-10-11 15:46:49 |
to clarify, that's  = = 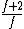
|
|  | jax
2005-12-05 19:41:50 | On my exam the ln (natural log) looks more like 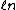 . Is that just a misprint? At first I crossed out this answer choice because I didn't know what the variable . Is that just a misprint? At first I crossed out this answer choice because I didn't know what the variable 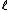 was and I thought ETS was trying to trick people into thinking it was a ln. None of the other answer choices worked though so I had to check here. Does anybody else notice this on their exam? was and I thought ETS was trying to trick people into thinking it was a ln. None of the other answer choices worked though so I had to check here. Does anybody else notice this on their exam?
yosun
2005-12-06 19:21:33 |
jax: it's not a misprint. i have the curly-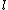 for ln on my GR9277 exam too. you shouldn't cross out choices based on funny looking print. moreover, you should understand the difference between isothermal/baric/sentric/choric work for an ideal gas. for ln on my GR9277 exam too. you shouldn't cross out choices based on funny looking print. moreover, you should understand the difference between isothermal/baric/sentric/choric work for an ideal gas.
|
jax
2005-12-06 21:06:06 |
I only have a curly l in one ln on the exam, all the other lns look normal, so I guess it IS a misprint (the fault of ETS).
I actually went back when I was doing the problem and I noticed that all of the other lns in other problems had a regular L. weird.
I do understand the problem though. Just confused about the 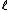 . .
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
