|
GR9277 #69
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Ryry013
2018-10-25 12:05:41 | My half-BS solution: I tried to figure out which of the answers could reasonably come from 1.5. I thought 1.5 = 3/2, saw 2/3, and then picked it. A guessing strategy for if you know zero Physics. |  | natec
2013-09-03 10:52:30 | when I first read this problem, I thought the particle was entering the glass. The word perpendicular lead me to that assumption. I guess the particle was already in the glass and emitting the Cherenkov Radiation. Since I thought the particle was entering the glass, I thought this was a question about Bremsstrahlung (breaking) radiation. |  | hjq1990
2012-10-02 23:16:55 | Seems that I misunderstood this question at first, wondering the relation of the initial speed of particle and the energy of the emitted light. After reading your notes, I think what matters is that the particle has to be moving in a velocity bigger than the medium speed in order to emit. This speed is a minimal and we need not consider any rigid conservation here. | | Tritium
2010-09-19 21:50:13 | It seem like this question is improperly formed. The question states only that a fast particle travels through a medium with an index of refraction n = 1.5 and emits light. Why must the particle's MINIMUM speed equal the speed of light in the medium (c/n = 0.67c)? What is to prevent the particle from traveling at half the speed of light, while emitting light that travels within the medium at the speed c/n = 0.67c? This question would make sense if it said the particle emits a CONE of light. Then we would know the particle was giving off Cerenkov radiation, and must be traveling faster than c/n. Am I misunderstanding the question? | | dicerandom
2006-10-25 18:19:22 | Wait... what? The minimum speed the particle can have is the maximum speed it could possibly obtain? And it emits light because it actually went faster than that?
When I read this I figured light was emitted because the thing knocked into an atom and excited an electron which then dropped down a level or two and radiated.
Shoshe
2006-11-03 15:33:19 |
Your assumption of "The minimum speed the particle can have is the maximum speed it could possibly obtain" isn't right. The maximum speed the particle could possibly obtain is  , the speed of light in a vacuum. Nothing prevents a particle traveling through a medium from going faster than the ) . Cherenkov radiation is emitted when a charged particle's velocity in a medium is greater than the speed of light in that medium. So the charged particle in this question must be going faster than  .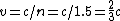
|
|  | poop
2005-11-23 15:42:12 | FYI, this phenomenon is called "Cherenkov Radiation"
yosun
2005-11-23 15:56:55 |
FYI: Cherenkov Radiation occurs when the particle travels faster than the speed of light in the medium. A particle emits light when it makes transitions from level to level, but since this is a free particle, the only way it can emit light is through Cherenkov Radiation.
|
gt2009
2009-05-20 10:37:56 |
Why are there so many people named poop on here?
|
Albert
2009-10-21 08:05:09 |
Did you not think that there could be just one person named poop who is writing all those posts?
Use it, its more than just a hat rack :)
|
his dudeness
2010-09-04 19:17:48 |
my personal favorite is "poop loops"
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
