|
GR9277 #94
|
|
|
|
|
Alternate Solutions |
ramparts
2009-08-16 17:32:18 | Make it one step simpler - they're kind enough to give you natural units (c=1), so the Lorentz transformations for x and t are exactly the same - just switch your x's and t's (primes left intact). Equation 3 looks like that. Great!
Just like the official solution, but no need to factor anything out.
Calculating spacetime intervals seems.... a bit much for this test. |  | student2008
2008-10-16 13:54:16 | LOL! The simplest way here is to calculate the interval 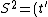^2-(x')^2) , it should be equal to , it should be equal to 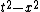 . This can't be true for (A) & (B), and in (D) . This can't be true for (A) & (B), and in (D) 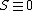 . But, it is correct for (C). . But, it is correct for (C).
In general situation (i.e. when y's and z's also change) this is the only practical method. You would get stuck using the general form of transformations. |  |
|
|
Comments |
nyuko
2009-10-30 22:32:21 | I did this problem by:
(1) x and t transform in the same way (c=1)
(2)  has to be greater than 1 has to be greater than 1
then the answer is (C)
However, now I look back at the choices; there is a choice (E) so we need to check if 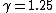 and and 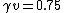 are corresponding to the same relative velocity of frame...and then I guess ETS does not want us to check the math but just to know (1) and (2) I stated above? are corresponding to the same relative velocity of frame...and then I guess ETS does not want us to check the math but just to know (1) and (2) I stated above? |  | ramparts
2009-08-16 17:32:18 | Make it one step simpler - they're kind enough to give you natural units (c=1), so the Lorentz transformations for x and t are exactly the same - just switch your x's and t's (primes left intact). Equation 3 looks like that. Great!
Just like the official solution, but no need to factor anything out.
Calculating spacetime intervals seems.... a bit much for this test. |  | ramparts
2009-08-16 17:32:02 | Make it one step simpler - they're kind enough to give you natural units (c=1), so the Lorentz transformations for x and t are exactly the same - just switch your x's and t's (primes left intact). Equation 3 looks like that. Great!
Just like the official solution, but no need to factor anything out.
Calculating spacetime intervals seems.... a bit much for this test. |  | CaspianXI
2009-03-19 15:59:11 | If you're low on time, here's an easy way to solve this problem.
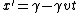
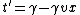
Thus, the first terms in both x' and t' must be the same. And the coefficients of the second terms for both x' and t' must be the same. (C) is the only one which satisfies this, so you're done.
CaspianXI
2009-03-20 20:55:39 |
Oops... typo. I *meant* to list the equations as:
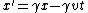
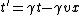
The rest of the logic still applies.
WARNING: 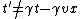 in general. This is only true because we've been given that we're using some funky units where c = 1. in general. This is only true because we've been given that we're using some funky units where c = 1.
|
ramparts
2009-08-06 23:20:57 |
They're not funky units, they're natural! ;) Thank God for natural units, too. The c's are so unseemly.
|
|  | tinytoon
2008-11-07 02:18:56 | I think Yosun's solution is valid, but the easiest way to do it is to recognize that Lorentz transformations are the following:
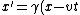)
and
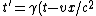)
In units of c = 1, which the problem kindly gives us, the second transformation becomes:
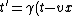)
Now we can clearly see that the  's and the 's and the  's are symmetrical in the two transformations and out pops (C). 's are symmetrical in the two transformations and out pops (C). |  | student2008
2008-10-16 13:54:16 | LOL! The simplest way here is to calculate the interval 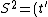^2-(x')^2) , it should be equal to , it should be equal to 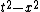 . This can't be true for (A) & (B), and in (D) . This can't be true for (A) & (B), and in (D) 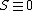 . But, it is correct for (C). . But, it is correct for (C).
In general situation (i.e. when y's and z's also change) this is the only practical method. You would get stuck using the general form of transformations.
neon37
2008-10-29 01:52:17 |
Note: ds=0 for light.
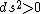 space-like space-like
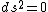 null null
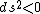 time-like time-like
|
|  | FortranMan
2008-10-12 08:58:48 | you can eliminate D by remembering that  must be greater than 1. To absolutely eliminate E, note that here must be greater than 1. To absolutely eliminate E, note that here 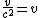 , then double check , then double check  . . |  | evanb
2008-06-26 19:37:47 | Actually, that's not enough to satisfy that it's a Lorentz transformation.
Consider:
x' = 10x - 1t
t' = 10t - x
According to the official solution, this would be a Lorentz transformation with 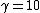 and and 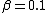 , but we can check that such a transformation is unphysical: , but we can check that such a transformation is unphysical:  and and 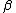 are not independent, and because are not independent, and because
$\frac{1}{\sqrt{1-\beta^2}} = \frac{1}{\sqrt{1-0.1^2}} = \frac{1}{\sqrt{0.99}} << 10 = \gamma$, this is not a legit Lorentz transform.
However, since the numbers here --happen-- to be 5/4 and 3/4, we're in the clear.
Maxwells_Demon
2008-09-21 17:12:38 |
Wait, how are we in the clear??????? If gamma really is 5/4 then beta should be 3/5. Beta is clearly 3/4 = 0.75
So how is it a valid transformation?
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
