GREPhysics.NET: GR9277 #99

GR9277 #99

Problem

GREPhysics.NET Official Solution

\prob{99}
In perturbation theory, what is the first order correction to the energy of a hydrogen atom (Bohr radius $a_0$ ) in its ground state due to the presence of a static electric field E?

0
$eEa_0$
$3eEa_0$
$\frac{8e^2Ea_0^3}{3}$
$\frac{8e^2E^2a_0^3}{3}$

Quantum Mechanics $\Rightarrow$ }Perturbation Theory

The perturbed Hamiltonian is given by $\Delta H = eEz = eEr\cos\theta$ , where the last substitution is made for spherical coordinates.

The first-order energy-shift is given by $\langle \psi_0 | \Delta H | \psi_0 \rangle$ , where $\psi_0\propto e^{-kr}$ .

$dV=r^2drd\Omega=r^2\sin^2\theta d\phi d\theta dr$ .

Thus, $E_0 = \int_0^\infty \int_0^{\pi} \int_0^{2\pi} e^{-kr}\cos\theta\sin^2\theta d\theta d\phi =0$ , since the integral of $\cos\theta\sin^2\theta$ over $0$ to $\pi$ is 0.

Search this site for keyword perturbation for more on this.

Alternate Solutions

evanb
2008-06-27 14:46:04

The wave function of 1s is even, the perturbative operator = - q * Efield * Z is odd.

Thus the first-order matrix element must be zero.

Reply to this comment

Comments

evanb
2008-06-27 14:46:04

The wave function of 1s is even, the perturbative operator = - q * Efield * Z is odd.

Thus the first-order matrix element must be zero.

nyuko
2009-10-30 23:05:54

I want to post the same thing as you did. But you are one year ahead of me :)

Reply to this comment

zzzzort
2007-11-01 14:26:58

None of the other answers have the correct units.

jburkart
2007-11-02 00:48:27

No, electric field times charge is force, and force times distance is work, a form of energy. You have to do it the proper way.

Reply to this comment

herrphysik
2006-09-14 23:08:00

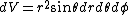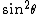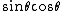Minor typo: In spherical coordinates $dV = r^2 sin{\theta} dr d \theta d \phi$ (not $sin^2{\theta}$ ) and the limits for theta are 0 to 2*pi. And of course the integral of $sin{\theta} cos{\theta}$ from 0 to 2*pi is 0.

E^2Pi-1=0
2006-11-30 19:34:06

The limit is still 0 to pi ... theta is azimuthal angle.... but integral of Sin[theta]Cos[theta] from 0 to pi is still zero.....

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 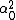$\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
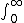$\partial$	$\partial$
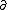$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
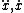$\sqrt{z}$	$\sqrt{z}$
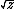$\langle my \rangle$	$\langle my \rangle$
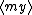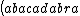$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
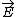$\frac{a}{b}$	$\frac{a}{b}$

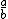The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone