|
This problem is still being typed. |
Quantum Mechanics }Scattering }Scattering
This is a conceptual scattering question. No calculations needed.
(A) A particle incident from the left would have an oscillating wave function until it meets the barrier... not the other way around.
(B) For 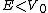 , It is true that the barrier would decrease the amplitude of the wave function, however, when it emerges, the tunneled part of it should have an even smaller amplitude. (This graph would be good for , It is true that the barrier would decrease the amplitude of the wave function, however, when it emerges, the tunneled part of it should have an even smaller amplitude. (This graph would be good for 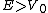 , however.) , however.)
(C) This is the only graph that shows the wanted characteristics: oscillating wave before incidence, decay while in barrier, and tunneled-decrease amplitude when exit.
(D) A typical particle is probably least likely to be found inside the barrier, so this is the least likely choice.
(E) This wave function shows no change, when the potential barrier demands a change!
|
