|
GR9677 #6
|
|
|
|
|
Alternate Solutions |
insertphyspun
2011-02-06 13:05:22 | A way to rule out answers, although not the fastest strategy:
A) Wrong. The limit as 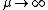 gives us no loss in energy, which is just weird. If you can't remember the answer, you would at least think it should be proportional to or independent of gives us no loss in energy, which is just weird. If you can't remember the answer, you would at least think it should be proportional to or independent of 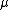 . .
B) Maybe. Keeping your logic from (A), this one stays in the running.
C) Wrong. As 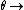 0, the plane becomes a flat surface. The block will only move at a constant velocity if there is no dissipative force (since we know there is no applied force). This implies no energy loss. The limit for this answer gives us infinite energy loss, which is crazy. 0, the plane becomes a flat surface. The block will only move at a constant velocity if there is no dissipative force (since we know there is no applied force). This implies no energy loss. The limit for this answer gives us infinite energy loss, which is crazy.
D) Wrong. The limit as 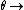 0 at first gives us a reasonable answer (i.e. if the track is flat and there is no applied force, the block should not lose energy if it moves at a constant velocity). However, in order to move at a constant velocity on a flat surface in the absence of an applied force, there cannot be friction. The problem states that there is friction, so this doesn't add up. 0 at first gives us a reasonable answer (i.e. if the track is flat and there is no applied force, the block should not lose energy if it moves at a constant velocity). However, in order to move at a constant velocity on a flat surface in the absence of an applied force, there cannot be friction. The problem states that there is friction, so this doesn't add up.
E) Wrong. We know there is a non-conservative force in the problem, therefore work is being done. There must be a change in energy.
So, the answer is (B). This definitely takes longer than the energy arguments, but may be faster than considering a force diagram.
|  | 99percent
2008-11-06 06:25:06 | An easy way...
Since, the speed of the block is constant, there is no gain in the kinetic energy of the block.
Thus, potential energy lost by the block = Energy dissipated by friction = mgh.
Bingo..!!
|  |
|
|
Comments |
fredluis
2019-08-08 06:59:38 | Well , The total resultant force on the car is in the radial direction. Obviously you have a drag force backwards. tree trimming |  | enterprise
2018-04-01 14:07:45 | mgh at the top must appear as a potential energy at the bottom. Because , this isn\'t so , the energy must go somewhere as a thermal energy due to friction. |  | exenGT
2012-10-10 04:24:21 | Consider the total energy of the block:
At top: 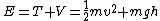 ; ;
At bottom: 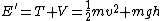 (since block moves at constant speed) (since block moves at constant speed)
But total energy of the system (block+ramp) is conserved
Therefore the energy dissipated by friction 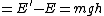 . .
exenGT
2012-10-10 04:28:37 |
Consider the total energy of the block:
At top: 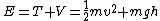 ; ;
At bottom: 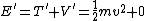 (since block moves at constant speed) (since block moves at constant speed)
But total energy of the system (block+ramp) is conserved;
Therefore the energy dissipated by friction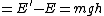 . .
(Sorry that my previous post contains several typos; please ignore that post.)
|
|  | insertphyspun
2011-02-06 13:05:22 | A way to rule out answers, although not the fastest strategy:
A) Wrong. The limit as 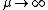 gives us no loss in energy, which is just weird. If you can't remember the answer, you would at least think it should be proportional to or independent of gives us no loss in energy, which is just weird. If you can't remember the answer, you would at least think it should be proportional to or independent of 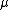 . .
B) Maybe. Keeping your logic from (A), this one stays in the running.
C) Wrong. As 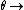 0, the plane becomes a flat surface. The block will only move at a constant velocity if there is no dissipative force (since we know there is no applied force). This implies no energy loss. The limit for this answer gives us infinite energy loss, which is crazy. 0, the plane becomes a flat surface. The block will only move at a constant velocity if there is no dissipative force (since we know there is no applied force). This implies no energy loss. The limit for this answer gives us infinite energy loss, which is crazy.
D) Wrong. The limit as 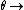 0 at first gives us a reasonable answer (i.e. if the track is flat and there is no applied force, the block should not lose energy if it moves at a constant velocity). However, in order to move at a constant velocity on a flat surface in the absence of an applied force, there cannot be friction. The problem states that there is friction, so this doesn't add up. 0 at first gives us a reasonable answer (i.e. if the track is flat and there is no applied force, the block should not lose energy if it moves at a constant velocity). However, in order to move at a constant velocity on a flat surface in the absence of an applied force, there cannot be friction. The problem states that there is friction, so this doesn't add up.
E) Wrong. We know there is a non-conservative force in the problem, therefore work is being done. There must be a change in energy.
So, the answer is (B). This definitely takes longer than the energy arguments, but may be faster than considering a force diagram.
|  | petr1243
2010-12-28 09:08:42 | I did the problem a slightly different way:
A frictional force is an example of a non-conservative force, so this is a non-isolated system:
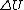 + + 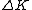 = -(f_k)L = -(f_k)L
Assuming that the particle starts and ends at rest:
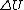 = mgh = mgh
mgLsin(theta) = - (mu_k)mgcos(theta)L
Coefficient of Kinetic Friction is: mu_k = -tan(theta)
The work done by the frictional force is:
W = 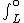 f_k*dx f_k*dx
W = -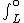 mgsin(theta)dx mgsin(theta)dx
W=mgLsin(theta) = mgh |  | Niko
2010-11-07 09:15:55 | Yeah... just remember that when non-conservative forces are involved, the change in mechanical energy is equal to the work done by non-conservative forces (friction in this case).
The key phrase here is "constant speed" which means constant KE. The change in mechanical energy (Umech = KE + PE with KE=const) is just mgh.
A tricky one to get under pressure. |  | 99percent
2008-11-06 06:25:06 | An easy way...
Since, the speed of the block is constant, there is no gain in the kinetic energy of the block.
Thus, potential energy lost by the block = Energy dissipated by friction = mgh.
Bingo..!!
Saint_Oliver
2013-09-23 08:36:52 |
Winner
|
justin_l
2013-10-17 22:59:50 |
this is the best answer and is probably the answer they are looking for.
Mechanical Energy before: mgh
Mechanical Energy after: 0
where did it go?
into friction.
|
Ryry013
2019-05-26 15:30:53 |
Slightly more accurate would be:\r\n\r\nEnergy before: 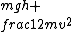 \r\nEnergy after: \r\nEnergy after: 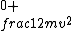 (same velocity throughout)\r\n\r\nThen, the mgh-->0 part all went into friction, as you all said. (same velocity throughout)\r\n\r\nThen, the mgh-->0 part all went into friction, as you all said.
|
|  | cyberdeathreaper
2006-12-28 19:42:46 | Isn't it somewhat repetitive to solve for the coefficient of kinetic friction, to plug back in to solve for friction, to calculate work? Couldn't you solve for f from your x-coordinate forces (f=mgsin(theta)), and plug that straight into your work equation (W=fl)?
microcentury
2010-07-12 07:40:41 |
Very true.
W= F*l = mg sin(theta)*L.
Since h= L*sin(theta), we have W=mgh
|
|  | daschaich
2005-11-07 23:22:21 | There's an easier way to do it - conservation of energy. Since the speed of the block is constant, its kinetic energy is the same at the top and bottom of the ramp. Therefore all its gravitational potential energy (mgh) must have been dissipated by friction.
Blake7
2007-09-22 08:04:31 |
Excellent observation; saves a tremendous amount of time with much less risk.
|
dcan
2008-04-09 17:11:02 |
This seems so obvious after seeing the answer. It's hard to get out of the crunch mode.
|
tau1777
2008-11-05 14:49:47 |
all i could say after reading this was:quite beautiful. this is an excellent solution, thank you for sharing.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
