|
GR9677 #72
|
|
|
Problem
|
|
|
This problem is still being typed. |
Lab Methods }Negative Feedback }Negative Feedback
Negative feedback, according to Horowitz's The Art of Electronics, has to do with canceling out some of the input in the output. Although that might seem like redundantly adding noise to the system, it actually reduces the amplifier's gain, increases stability (by decreasing nonlinearity and distortion).
From that bit of info, two choices remain. Choice (A) and (B). Choose (A) because negating the feedback should not increase the amplitude.
|
|
|
Alternate Solutions |
CaspianXI
2009-03-28 09:40:43 | Being that this is an electronics problem, if you happen to have an interest in how electronics work (regardless of whether you've studied feedback in a formal course), you can make this problem easy on yourself.
There are two types of feedback -- negative and positive. Positive feedback is what happens when you place a microphone next to a speaker and you get the squealing sound. Sounds go into the microphone, get amplified, and come out of the speaker. These sounds then get fed back into the microphone (hence the name "feedback"), get amplified again, and come out even louder out of the speaker. The sound grows, resulting in quite a bit of amplification.
When you hear positive feedback, think of how a speaker squeals when the microphone gets too close. When you hear negative feedback, think of noise cancellation. Positive feedback is adding a "copy" of a wave to itself, essentially doubling its amplitude. Negative feedback is adding the "negative of a copy" of a wave to itself -- effectively subtracting a wave from itself, resulting in de-amplification.
Hence, negative feedback can never increase amplification. |  |
|
|
Comments |
droosenoose
2019-10-22 23:07:47 | this is a bit misleading because you can easily use negative feedback to amplify signal if you have an op amp and two resistors, which is what I immediately thought of when they said negative feedback.\r\nGuess they were referring to the concept of negative feedback itself, not applications?? |  | CaspianXI
2009-03-28 09:40:43 | Being that this is an electronics problem, if you happen to have an interest in how electronics work (regardless of whether you've studied feedback in a formal course), you can make this problem easy on yourself.
There are two types of feedback -- negative and positive. Positive feedback is what happens when you place a microphone next to a speaker and you get the squealing sound. Sounds go into the microphone, get amplified, and come out of the speaker. These sounds then get fed back into the microphone (hence the name "feedback"), get amplified again, and come out even louder out of the speaker. The sound grows, resulting in quite a bit of amplification.
When you hear positive feedback, think of how a speaker squeals when the microphone gets too close. When you hear negative feedback, think of noise cancellation. Positive feedback is adding a "copy" of a wave to itself, essentially doubling its amplitude. Negative feedback is adding the "negative of a copy" of a wave to itself -- effectively subtracting a wave from itself, resulting in de-amplification.
Hence, negative feedback can never increase amplification.
jmason86
2009-09-28 18:02:16 |
Now that's my kind of solution!
Thanks!
|
Froe
2012-11-05 01:38:03 |
Great! Thank you!
|
|  | physicsisgod
2008-10-30 12:58:45 | For the mathematically inclined:
Commonly, a voltage amplifier multiplies the input voltage by some open-loop positive constant, called the gain, or amplification:
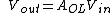
If we apply a negative feedback loop to the amplifier, we send a new input voltage to be amplified by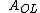 ; namely, the new input voltage is the original input voltage minus some fraction of the output voltage: ; namely, the new input voltage is the original input voltage minus some fraction of the output voltage:
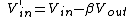
Therefore, the new output voltage is
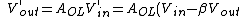)
Thus, 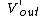 < < 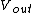 , or , or 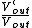 < 1, so the amplification cannot increase. < 1, so the amplification cannot increase. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
