|
GR9677 #76
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Uncertainty }Uncertainty
One can make a good stab at this problem by applying the uncertainty principle.
I. If the average momentum of the packet is 0, then one violates the uncertainty principle. See IV.
II. Maybe.
III. Maybe.
IV. True, recall the Gaussian uncertainty principle 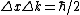 . .
Since I is false, choices (A), (C), and (E) are out. Choices (B) and (D) remain. Take the conservative approach and choose (B).
|
|
|
Alternate Solutions |
ETScustomer
2017-10-03 19:27:24 | One can maybe eliminate I. by this line of thought: Pretend that the packet is not really moving that much. Then, you start moving really fast (but not too fast!). The packet should look to you like it\'s moving pretty fast in the direction opposite of your motion. That fast moving Gaussian packet had better not have zero overall momentum! |  | kaic
2013-10-15 16:33:09 | Unfortunately if you don't know much about gaussian wave packets this problem can be pretty tricky. Here's an explanation.
(A) This would violate uncertainty, the average momentum of the wave packet is related to the (very small) average position via the uncertainty relation, so that it is finite.
(B) Since the uncertainty in momentum is very large, it can be thought of as a superposition of many waves all propagating with different momenta. Thus as time goes on, the width of the wave (its expected position) spreads out, as each wave in the packet travels at a slightly different speed.
(C) Recall that a normalized wave function remains normalized. Thus the integral over all space of 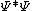 is invariant as time goes on, so as the wave function spreads out, its amplitude decreases. Again, think of the wave as a superposition of waves with different momenta. At first they are all closely spaced, and their amplitudes add according to superposition. As they spread out, their amplitudes are spread out as well, so they don't all add up to a large spike at the center. is invariant as time goes on, so as the wave function spreads out, its amplitude decreases. Again, think of the wave as a superposition of waves with different momenta. At first they are all closely spaced, and their amplitudes add according to superposition. As they spread out, their amplitudes are spread out as well, so they don't all add up to a large spike at the center.
(D) This follows trivially from the uncertainty principle. This one is really the key, as you can confirm or deny the other three based on knowledge of this one, but you have to think really hard about it, and sadly the GRE isn't testing you on how well you can actually think about physics. |  | blackerester
2012-04-19 23:27:01 | Here's the cheap and dirty way to do. Zero, and I do mean zero, physics knowledge required. The frequency of appearance of each statement in the possible answers breaks down as follows:
I -> 3 times
II -> 4 times
III -> 3 times
IV -> 4 times
We choose the most frequent statements II and IV and thus we have (B). I'm not saying it's a good strategy, but logically speaking, the correct answers will appear more often so that they can catch you when you're only sure about some statements. |  | pablojm
2006-10-28 16:03:06 | I think buddy.epson's argument is even better than the original one, since can be 0 and not violate the uncertainty principle. This is because the uncertainty principle relates standard deviations, and the standard deviation of p is sqrt(-^2). Thus, you could have different from 0, so the average momentum is 0 and the uncertainty principle holds. However, the problem says that the statements should be correct for ALL wave packets, and if we have a wavepacket which starts motion to the right, its average momentum will continue to be to the right for all time because it's in free space. |  |
|
|
Comments |
whereami
2018-04-06 02:01:22 | i see some people are saying average momentum can\'t be zero due to uncertainty principle. But that has nothing to do with principle. average momentum is not delta p. Option I is wrong because average momentum can be not zero. there is no reason its momentum should be fixed to zero. |  | ETScustomer
2017-10-03 19:27:24 | One can maybe eliminate I. by this line of thought: Pretend that the packet is not really moving that much. Then, you start moving really fast (but not too fast!). The packet should look to you like it\'s moving pretty fast in the direction opposite of your motion. That fast moving Gaussian packet had better not have zero overall momentum! |  | dydtaylor
2015-10-21 14:41:12 | Correct me if I\'m wrong but wouldn\'t (II) and (III) both being correct break normality?\r\n\r\nThat narrows it down to A, and B, but we know (IV) should be true from the uncertainty principle, implying we should take B over A. |  | calvin_physics
2014-03-27 14:16:07 | Here's how I view it. rnrn1. If the average momentum = 0. then the wave isn't traveling. So this can't be right.rn2. Maybern3. Maybe rn4. Uncertainty Principle must be correct. rnrnHowever, 2 and 3 are mutually exclusive. If the width increases, A can't be constant. If A is constant, width won't increase.rnChoose an answer that has 4 and either 2 or 3, not both. |  | kaic
2013-10-15 16:33:09 | Unfortunately if you don't know much about gaussian wave packets this problem can be pretty tricky. Here's an explanation.
(A) This would violate uncertainty, the average momentum of the wave packet is related to the (very small) average position via the uncertainty relation, so that it is finite.
(B) Since the uncertainty in momentum is very large, it can be thought of as a superposition of many waves all propagating with different momenta. Thus as time goes on, the width of the wave (its expected position) spreads out, as each wave in the packet travels at a slightly different speed.
(C) Recall that a normalized wave function remains normalized. Thus the integral over all space of 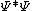 is invariant as time goes on, so as the wave function spreads out, its amplitude decreases. Again, think of the wave as a superposition of waves with different momenta. At first they are all closely spaced, and their amplitudes add according to superposition. As they spread out, their amplitudes are spread out as well, so they don't all add up to a large spike at the center. is invariant as time goes on, so as the wave function spreads out, its amplitude decreases. Again, think of the wave as a superposition of waves with different momenta. At first they are all closely spaced, and their amplitudes add according to superposition. As they spread out, their amplitudes are spread out as well, so they don't all add up to a large spike at the center.
(D) This follows trivially from the uncertainty principle. This one is really the key, as you can confirm or deny the other three based on knowledge of this one, but you have to think really hard about it, and sadly the GRE isn't testing you on how well you can actually think about physics. |  | blackerester
2012-04-19 23:27:01 | Here's the cheap and dirty way to do. Zero, and I do mean zero, physics knowledge required. The frequency of appearance of each statement in the possible answers breaks down as follows:
I -> 3 times
II -> 4 times
III -> 3 times
IV -> 4 times
We choose the most frequent statements II and IV and thus we have (B). I'm not saying it's a good strategy, but logically speaking, the correct answers will appear more often so that they can catch you when you're only sure about some statements.
dragore
2012-08-16 11:21:57 |
I like this.
|
physgre
2015-10-20 10:42:39 |
牛逼
|
|  | faith
2010-11-05 19:59:15 | i do not understand how 3 is wrong. here's a link
http://demonstrations.wolfram.com/EvolutionOfAGaussianWavePacket/
faith
2010-11-05 20:01:28 |
remove http:// to access the site.
|
flyboy621
2010-11-05 20:48:25 |
Well, the total area under the curve has to remain constant. So as the width increases with time, the height must decrease.
|
|  | sullx
2009-11-03 19:29:42 | For the visual learners:
http://rugth30.phys.rug.nl/quantummechanics/potential.htm
I watched these videos a few days before I took 9677 and I answered this problem correctly because of it.
|  | wangjj0120
2008-09-24 06:24:43 | I don't understand~the wave packet is traveling through "free space", it's a non-dispersive medium. Waves with different  and and 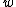 propagate with propagate with 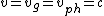 , from this point the wave packet should maintain its shape. What wrong with this point of view? , from this point the wave packet should maintain its shape. What wrong with this point of view?
flyboy621
2010-11-05 20:51:42 |
Your argument applies to an ideal plane wave, but a plane wave is not physically realistic because it extends infinitely through space. We study plane waves because they make good approximations to a lot of physical systems, and are easy to work with. But a real wave behaves like a packet with a spread of 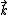 and and 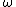 values. values.
|
|  | jburkart
2007-11-02 18:04:15 | I thought along the lines of: [II] and [III] can't both be true, since if it's getting wider, due to normalization, its amplitude must be decreasing, so I could eliminate choices (D) and (E). [IV] I knew was true, from the uncertainty principle, so I eliminated (A). Lastly, [I] seemed highly suspect, and [II] and [III] both seemed about equally probable, so I went with the higher probability choice of (B).
99percent
2008-11-06 08:03:38 |
This is correct...
A gaussian wavepacket always expands in free space.. Thus, II is definitely true..!!
Now since II is correct, III has to be false..!!
Bingo..!!
For a better and more detailed explanation check this journal at IOP...
http://www.iop.org/EJ/abstract/0143-0807/18/3/022
" target="_blank">http://www.iop.org/EJ/abstract/0143-0807/18/3/022">http://www.iop.org/EJ/abstract/0143-0807/18/3/022
|
jmason86
2009-10-01 19:52:38 |
Also, I may seems suspect seen momentum is is a description of something velocity, and this is a "wave packet that TRAVELS through free space". So the average momentum shouldn't be zero.
|
|  | dumbguy
2007-10-17 14:45:10 | I have never heard of a wave that has a constant amplitude. Doesn't as time goes on, the amplitude fluxuate back and forth? So isn't this enough reason to rule III as false? let me know
sawtooth
2007-10-29 09:30:13 |
By amplitude, usually we mean the maximum of the disturbance (some call this the peak amplitude). As I know it, amplitude is the coefficient 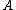 e.g. in the following wavefunction: e.g. in the following wavefunction: =Asin(\omega t - k x)) . When . When 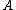 doesn;t depent on doesn;t depent on 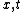 we call it constant. Ofcourse, the displacement (or whatever the oscillating "thing" is) fluxuates. we call it constant. Ofcourse, the displacement (or whatever the oscillating "thing" is) fluxuates.
At least this is the case in this exercise-and usually it's used this way in quantum mechanics.
|
|  | shoyer
2007-08-05 22:40:59 | I have a reason for the guess in the last stage of the official answer.rnrnOnce eliminate I and have decided that IV is true, you have two options: B or D. (II and IV or II, III and V).rnrnIf II must be true, then the wave spreads out. In that case, then amplitude remaining the same over time would mean that the total probability of measuring the wave packet integrated over all space would increase beyond 1. Since this can't be true, eliminate answer D. |  | pablojm
2006-10-28 16:03:06 | I think buddy.epson's argument is even better than the original one, since can be 0 and not violate the uncertainty principle. This is because the uncertainty principle relates standard deviations, and the standard deviation of p is sqrt(-^2). Thus, you could have different from 0, so the average momentum is 0 and the uncertainty principle holds. However, the problem says that the statements should be correct for ALL wave packets, and if we have a wavepacket which starts motion to the right, its average momentum will continue to be to the right for all time because it's in free space. |  | buddy.epson
2006-10-14 11:05:28 | I eliminated statement I by reasoning that a bound particle (e.g. in a 1-D well) could have time-avg'd momentum of zero as it bounces back and forth in the well, but a free particle would travel in one direction and hence have a nonzero avg. momentum.
After reading yosun's explanation above, I am curious if my reasoning is flawed. I encourage discussion, as my quantum mech. knowledge is limited. |  | andreas
2005-11-10 03:46:31 | daschiach: True, and this can even be shown by IV. If anybody wants more info on this, check on the difference between Group and Phase velocity. For example:
http://en.wikipedia.org/wiki/Phase_velocity />
http://en.wikipedia.org/wiki/Group_velocity |  | daschaich
2005-11-08 23:22:33 | As for II, we know that a Gaussian wave packet is the superposition of waves of several different momenta, which will travel at different speeds as time goes on. So the wave packet will spread out as time passes.
This shows that III is false, since if the wave packet is spreading out, its peak amplitude has to decrease to keep things properly normalized.
Townsend has a nice discussion on pgs. 160-164 of his "A Modern Approach to Quantum Mechanics" book. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 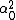 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
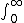 |
| $\partial$ |
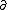 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
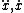 |
| $\sqrt{z}$ |
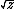 |
| $\langle my \rangle$ |
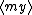 |
| $\left( abacadabra \right)_{me}$ |
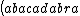_{me}) |
| $\vec{E}$ |
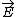 |
| $\frac{a}{b}$ |
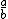 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
