|
GR9677 #98
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mike
2009-11-06 17:00:34 | Look at the 1992 test, problem 89...
I didn't know the ETS gave the same problems over |  | anmuhich
2009-04-02 12:16:25 | You can also immediately eliminate all but C and D because the energy can't be zero.
segfault
2009-08-19 20:32:07 |
Also (C) is just the energy levels of an unperturbed harmonic oscillator, so it has to be D.
|
cilginfizikci
2010-03-09 02:36:30 |
why the energy can not be "0" ??? dont tell me that this is harmonic oscillator... coz u already change the system... ????????????
|
carle257
2010-04-05 19:09:54 |
If the energy were zero, then this would imply that the position is zero because the harmonic oscillator potential goes as 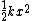 , and the kinetic term would also have to be zero to make the total energy zero ( ) But because of the uncertainty principle, we cannot simultaneously define the momentum and position to be zero.
Put another way, if the potential and thus position is zero, you would have a huge uncertainty in the momentum and thus the kinetic term would be non-zero.
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
|
