|
GR0177 #11
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
sophie
2014-10-21 00:23:22 | http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/lenseq.html#c3rnrnAccording to that, we are supposed to take anything on the left of lens 1 as negative. Why don't we then take the object distance of first lens as -40cm? rn
arifmujibur
2015-02-16 02:46:43 |
I don't think they meant that. Distance of any real object or image from the lens is positive. Though they may appear negative in coordinate.
|
|  | nvp10
2014-04-01 17:21:35 | i'm being a perfectionist but the lensmakers formula relates focal disance f to the radii of curvature of the surfaces of the lens. what we use here is the thin lens formula. |  | Quark
2011-09-23 15:27:01 | To clarify why the solution is not (C), but is in fact (A):
As some of you pointed out, if an object is located at the focal point of a lens, the image would focus at infinity. But after careful analysis, you can notice that the rays passing through the first lens never really actually focus at 10cm to the right of the second lens (focal point). This is just a simplification model we use to solve a problem. We say that if the second lens were not present, the image of the first lens would focus at this particular point. But the rays actually hit the second lens before they have a chance to focus 10cm to the right of the second lens, at which point the second lens focuses them at 5cm to the right of itself. I would encourage you to draw a careful ray diagram to convince yourself of this. The object for the second lens is a virtual object meaning, the light is not really focused at that point.
If there was a REAL object sitting at 10cm to the right of the second lens (focal point) and the 1st lens were was not present, then you are correct, the light would focus to the left of the second lens at infinity. But as the problem is stated, it is the combination of lenses that forms the final image.
So in using the correct sign conventions as pointed out in the solutions, you do indeed get the correct answer; A.
Hope this helps |  | gn0m0n
2008-11-05 22:57:50 | Can the sign convention be stated as: "If the image and object are on the same side, there is a negative distance; if not, both are postive"?
calcuttj
2014-09-22 05:44:27 |
For lenses this is true, the opposite is true for mirrors.
|
|  | sonnb
2008-09-06 01:18:37 | Draw the lenses to scale. Take a parallel ray from the tip of the object, thru the first lens and then thru the common focal point of the lenses. It will emerge parallel through the second lens. Take a second ray from the tip of the object thru the leftmost focal point of the first lens and then parallel thru the two lenses. It will emerge thru the second lense and then pass thru the its focal point. The two rays will converge half way between (and below) the rightmost lens and its focal point. Answer (A).
his dudeness
2010-09-25 06:13:20 |
I'm confused. When I draw the two rays you indicate, I have them converging at the bottom edge of the second lens. Can someone please clarify?
|
sonnb
2010-10-05 12:51:51 |
Draw the focal points to scale and you will see that the rays hit the second lens in different places.
|
|  | petr1243
2008-04-09 07:26:22 | reason for why d_1i is -40 cm:
d_o < f(real image)----> d_i >0
d_o > f(virtual image)----> d_i<0
|  | Blake7
2007-09-19 05:53:32 | When you go into a lensmaker's problem like this, save time by remembering this utilitarian form
s' = sf/(s-f)
instead of trying to use 1/s' + 1/s =1/f.
Watch (units are in centimeters)
s1 = 40
f1 = 20
s1' = 40x20/(40-20) = 40
40 - 30 = 10 => -10 (by convention) = s2
f2 = 10
s2' = -10x10/(-10-10) = -100/-20 = 5cm
You'll thank me later
Blake7
2007-09-19 22:32:04 |
Actually, calling this a 'lensmaker's equation' is incorrect (I remembered later on). What we are working with here is the "Thin lens formula".
The REAL "lensmaker's equation" takes into account the index of refraction of the lens and its radii of curvature.
Pardon my oversight.
|
|  | sharpstones
2006-12-01 17:36:04 | I don't understand, you say that if the distance is negative then it is on the right side of the lense. But when we get our final answer it is a positive 5cm yet we still say it's on the right side?
ericimo
2007-10-24 12:26:24 |
no, positive implies that the image is on the opposite side of the lens as the incident light from the object. if the light from the object comes through the lens' left side, a positive distance means it's on the right side of the lens.
even though the image from the first lens is right of the second lens (where the negative comes into play), the light passes through the second lens from the left side. so, positive S'2 means the final image is on the right side of lens 2.
it is confusing though.
|
Jeremy
2007-10-26 12:07:21 |
To be honest, this made no sense to me either. I used Halliday, Resnick, and Walker (7th ed.) to study geometrical optics the first time around. The rule that I picked up from that study was real images have positive image distances, whereas virtual images have negative image distances (the same rule can be applied to focal points and their focal lengths). This doesn't really speak to which side of the lens the image is on though. But if you think about it for a while, you'll see that what Giancoli says on page 841 makes sense:
"The image distance is positive if it is on the opposite side of the lens from where the light is coming; if it is on the same side, 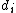 is negative. Equivalently, the image distance is positive for a real image and negative for a virtual image." is negative. Equivalently, the image distance is positive for a real image and negative for a virtual image."
Note that this convention is for use in "all situations," not just for converging lenses.
|
Jeremy
2007-10-26 13:30:50 |
To clarify, "all situations" really means "all lens configurations." For example, mirrors have the opposite sign convention: the image distance is positive if it is on the SAME side (reflecting side) of mirror as where the light is coming from; if it is on the OPPOSITE side (non-reflecting side, or "behind" the mirror), the image distance is negative.
|
vsravani
2008-10-04 22:30:49 |
As has been rightly pointed by Jeremy, with the sign convention of the images, if I go according to that, the answer that I would zero on is C.
My explanation:
Distance of the image formed by the first lens is 40cm on the right side of the first lens. Image is real and hence is positive.
This image is now object for the second lens which is 10 cm to the right side of the second lens. Implies that the object is at the focus of the second lens. We know that if the object is at the focus, the image is formed at infinity. So the option should be C
Kindly let me know if am right or wrong. And if wrong, where is the mistake
|
gryphia
2008-11-02 15:13:03 |
Positive is different for image and object locations. By convention (which makes the thin lens equation used here valid), an object has positive distance to the 'left' of a lens (left being the conventional side that has the light incident), and negative distance to the right (a virtual object, such as the one created by our first lens for our second), while an image has positive distance to the 'right' of a lens (right being the conventional side opposite the incident light), and negative distance to the left of a lens.
|
|  |
|
| Post A Comment! |
You are replying to:
To clarify why the solution is not (C), but is in fact (A):
As some of you pointed out, if an object is located at the focal point of a lens, the image would focus at infinity. But after careful analysis, you can notice that the rays passing through the first lens never really actually focus at 10cm to the right of the second lens (focal point). This is just a simplification model we use to solve a problem. We say that if the second lens were not present, the image of the first lens would focus at this particular point. But the rays actually hit the second lens before they have a chance to focus 10cm to the right of the second lens, at which point the second lens focuses them at 5cm to the right of itself. I would encourage you to draw a careful ray diagram to convince yourself of this. The object for the second lens is a virtual object meaning, the light is not really focused at that point.
If there was a REAL object sitting at 10cm to the right of the second lens (focal point) and the 1st lens were was not present, then you are correct, the light would focus to the left of the second lens at infinity. But as the problem is stated, it is the combination of lenses that forms the final image.
So in using the correct sign conventions as pointed out in the solutions, you do indeed get the correct answer; A.
Hope this helps
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
