|
GR0177 #16
|
|
|
Problem
|
|
|
This problem is still being typed. |
Lab Methods }Sample }Sample
The mean of the ten number is 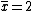 . Thus, the standard deviation of the sample is . Thus, the standard deviation of the sample is 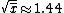 . (Search for Poisson Distribution on the site for another problem similar to this.) . (Search for Poisson Distribution on the site for another problem similar to this.)
If the student wants to obtain an uncertainty of 1 percent, then
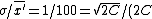=1/(\sqrt{2C})) , ,
where one assumes the average scales uniformly and C is the time to count. (Note: a good approximation of the uncertainty is given by the ratio of the standard deviation to the average, since that represents the deviation.)
Thus, one has 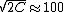 . Thus the student should count C=5000 s. . Thus the student should count C=5000 s.
A Sneak Peek of The Not-So-Boring Review of Undergrad Physics
(To be published in the to-be-posted library section of http://GREPhysics.NET in Feb 2006.)
The Poisson Distribution is intimately related to the raising and lowering operators of the (quantum mechanical) simple harmonic oscillator (SHO). When you hear the phrase ``simple harmonic oscillator," you should immediately recall the number operator 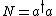 , as well as the characteristic relations for the raising , as well as the characteristic relations for the raising 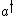 and lowering and lowering  and and 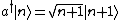 . And, don\'t forget the commutation relations that you should know by heart by now, . And, don\'t forget the commutation relations that you should know by heart by now, ![[a,a^{\dagger}]=1](/cgi-bin/mimetex.cgi?[a,a^{\dagger}]=1) . (That\'s all part of the collective consciousness of being a physics major.) . (That\'s all part of the collective consciousness of being a physics major.)
Now, here\'s some quasi-quantum magic applied to the Poisson Distribution. I\'m going to show you how to arrive at the result for standard deviation, i.e., 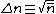 from using the SHO operators. from using the SHO operators.
Let\'s start with something easy to help jog your memory: The mean or average number in the distribution is just the expectation value of the Number operator, 
Okay! So, on with the fun stuff: the standard deviation is given by the usual definition, ^2 = \langle N^2 \rangle - \langle N \rangle^2) . .
The second term is already determined from the above expression for the mean, 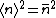 . .
The first term can be calculated from 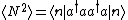 . Now, the commutation relation gives, . Now, the commutation relation gives, ![[a,a^{\dagger}]=1=aa^{\dagger}-a^{\dagger}a \Rightarrow aa^{\dagger}=a^{\dagger}a+1](/cgi-bin/mimetex.cgi?[a,a^{\dagger}]=1=aa^{\dagger}-a^{\dagger}a \Rightarrow aa^{\dagger}=a^{\dagger}a+1) . Replacing the middle two of the four a's with that result, the expression becomes . Replacing the middle two of the four a's with that result, the expression becomes 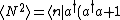 a |n \rangle = \langle n | a^{\dagger}a^{\dagger}aa + a^{\dagger}a |n \rangle = \langle n | a^{\dagger}a^{\dagger}aa | n \rangle + \langle n | a^{\dagger}a | n \rangle = \langle N \rangle^2 + \langle N \rangle = \bar{n}^2 + \bar{n} ) . .
Plugging the above results into the standard deviation, I present to you, this: ^2 = \bar{n}^2 - ( \bar{n}^2+\bar{n} ) = \bar{n} \Rightarrow (\Delta n) = \sqrt{\bar{n}}) . .
It\'s no coincidence that the above works. The secret lies in the energy eigenfunction that you might not remember...
\subsection{The Poisson Distribution Function is just =|\langle x | n\rangle|^2) The Poisson Distribution for a parameter The Poisson Distribution for a parameter 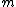 is given by is given by \propto e^{-m}\frac{m^\lambd}{\lambda!}) . But, wait, doesn\'t that look a wee bit too familiar? Indeed, the Poisson Distribution is merely the probability of obtaining . But, wait, doesn\'t that look a wee bit too familiar? Indeed, the Poisson Distribution is merely the probability of obtaining  photons at position photons at position  : : =|\langle x | n \rangle|^2) .\footnote{Note that since .\footnote{Note that since 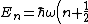) , each time n increases, it is like we've created an extra photon, since the energy of a photon is , each time n increases, it is like we've created an extra photon, since the energy of a photon is 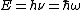 . Thus, . Thus,  represents the quanta.} represents the quanta.}
Why? So you ask. Well...
The energy eigenfunctions of the SHO is given by 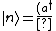^n}{(n!)^{1/2}} |0\rangle) , where , where 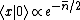 . .
This result can be arrived at in the position basis as follows: 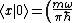^{1/4} e^{\frac{-m\omega x^2}{2\hbar}}) . The . The 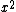 in the exponent can be re-expressed by the relation in the exponent can be re-expressed by the relation 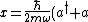) . Thus, . Thus, 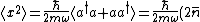) , where the other terms like , where the other terms like 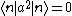 and we\'ve used the result for and we\'ve used the result for 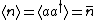 from above with the implicit assumption that its complex conjugate is the same, as the average photon number, from above with the implicit assumption that its complex conjugate is the same, as the average photon number, 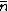 , is an observable. Thus, the exponent becomes , is an observable. Thus, the exponent becomes 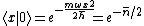 . .
The probability in the  -basis is thus, -basis is thus, =|\langle x | n \rangle|^2=\frac{\langle aa^\dagger \rangle}{n!}^{n} e^{-\bar{n}}=\frac{\bar{n}}{n!}^{n} e^{-\bar{n}}) , where using the definition , where using the definition 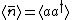 , we\'ve recovered exactly the Poisson Distribution for a parameter , we\'ve recovered exactly the Poisson Distribution for a parameter 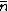 . .
Making the following associations, 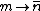 and and 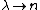 , you carve the first etchings in the Rosetta Stone between probability and photon statistics... , you carve the first etchings in the Rosetta Stone between probability and photon statistics...
|
|
|
Alternate Solutions |
NervousWreck
2017-03-28 09:45:40 | This is a very complicated problem due to the lack of time. However the fasters solution as I see it is the following\r\n=0.02) . Here rate is 2, which is multiplied by 1%. On the LHS is an error of poissson distribution with 2 measurements per second taken into account. The solution gives N = 5000, which now corresponds to seconds. . Here rate is 2, which is multiplied by 1%. On the LHS is an error of poissson distribution with 2 measurements per second taken into account. The solution gives N = 5000, which now corresponds to seconds. |  | redmomatt
2011-10-04 11:02:41 | Much easier way to think of this.
Approximate the variance, 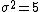 . .
Thus, the standard deviation is 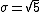 . .
Now, as N increases the error decreases by 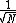 . .
Therefore, 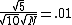  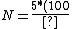^2}{10}=\frac{1}{2}\times10000=5000s) . . |  |
|
|
Comments |
Suman05eee
2017-10-12 08:25:50 | If we consider same mean for all different sized samples for this process, then :\r\n\r\nAccording Central Limit Theorem:\r\n\r\nSample SD=Population SD/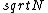 \r\n\r\nThus we can think of a sample of size N with the same SD (Calculated from the given sample of size 10= \r\n\r\nThus we can think of a sample of size N with the same SD (Calculated from the given sample of size 10=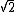 ) and get the Population SD= ) and get the Population SD=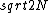 . And Mean = (Population SD)^2.= 2N.\r\nAnd at last use the uncertainty = Population Mean/ Population SD= 1/ . And Mean = (Population SD)^2.= 2N.\r\nAnd at last use the uncertainty = Population Mean/ Population SD= 1/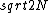 . . |  | NervousWreck
2017-03-28 09:45:40 | This is a very complicated problem due to the lack of time. However the fasters solution as I see it is the following\r\n=0.02) . Here rate is 2, which is multiplied by 1%. On the LHS is an error of poissson distribution with 2 measurements per second taken into account. The solution gives N = 5000, which now corresponds to seconds. . Here rate is 2, which is multiplied by 1%. On the LHS is an error of poissson distribution with 2 measurements per second taken into account. The solution gives N = 5000, which now corresponds to seconds. |  | ewcikewqikd
2014-07-05 14:52:10 | This problem is just statistics.
Suppose the standard deviation of the true population is  . .
The standard deviation of the mean of a sample of size 10 is expected to be 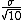 . .
The standard deviation of the mean of a sample of size n is expected to be 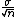 . .
Because the mean of the given sample is 2 and the question ask for uncertainty of 1%, we set 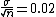
The standard deviation of the given sample is 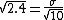
We can divide the two equations above to get 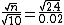
Solving for n, we get 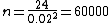
60000 measurements are needed! |  | redmomatt
2011-10-04 11:02:41 | Much easier way to think of this.
Approximate the variance, 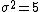 . .
Thus, the standard deviation is 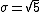 . .
Now, as N increases the error decreases by 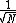 . .
Therefore, 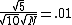  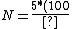^2}{10}=\frac{1}{2}\times10000=5000s) . .
rizkibizniz
2011-11-07 00:38:10 |
question: how have you come to approximate the variance as 5?
|
Rhabdovirus
2012-10-28 18:13:58 |
Riz: Variance is squared deviation so since the mean = 2, variance goes like ^2 + (0-2)^2+...}) which gives you which gives you 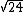 which is about 5. which is about 5.
|
luwei0917
2014-03-29 11:42:34 |
where 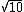 come from? come from?
|
|  | phoxdie
2010-11-12 21:40:21 | I have a quick question. When I looked at this the first time I arrived at the correct solution by the following method. First there are 10 measurements made, this is given. Next out of the ten the maximum spread is from 0 to 5 so I made the uncertainty in their measurement 5. Looking at the answers and what they are asking for, ie that the uncertainty be 1% I simply said 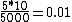 ie 1%. This turns out to be the correct answer (5000 seconds) but I am not sure if my naive method is legitimate or not. Does anyone think this is absolutely wrong, and I just got lucky or that there is something behind this? Thanks! ie 1%. This turns out to be the correct answer (5000 seconds) but I am not sure if my naive method is legitimate or not. Does anyone think this is absolutely wrong, and I just got lucky or that there is something behind this? Thanks! |  | wittensdog
2009-10-08 21:45:38 | The language of this problem is indeed pretty vague, so, here is one solution based on the way I interpreted it. I know there has already been a lot of talk on this, I hope maybe I can help sort things out a little...
First, if you just average all of those values, you get 2. So now I guess we just postulate that that should be close enough to the true average for us to get an idea of how long we should count for.
Now, in a Poisson distribution (which describes radioactive phenomenon, or most of it), we know that the standard deviation is the square root of the average. So we can take the standard deviation of this distribution to be sqrt(2). I don't know what the SD is if you actually calculate it for those numbers, but anyone who goes trying to calculate standard deviations from data on the GRE is completely insane.
Now, for reasons that can be seen if you take a course in statistics, the error on the mean is generally taken to be the standard deviation of the measurements divided by the square root of the number of measurements (this stems from the central limit theorem). I believe this is what is meant by uncertainty here. They state an uncertainty of one percent. I don't know exactly what it is that we want one percent of, but I'm guessing they mean 1% of the mean value, aka, the error on the mean should be plus or minus 1 percent of the mean. I don't know what else they would be referencing.
Since we are taking the mean as 2, or at least assuming it should be something in that ballpark, one percent of that would be 0.02. So if we know the standard deviation, the uncertainty we want, and the formula for the uncertainty on the mean, then we get,
uncert = SD / sqrt (n) ==>
0.02 = sqrt(2) / sqrt(n) ==>
4e-4 = 2/n ==>
n = 0.5 e +4 ==>
n = 5,000
So we want to make 5,000 measurements, and since each measurement is one second long, this corresponds to 5,000 seconds.
I hope this manages to help someone (and that I'm actually doing it right!).
Prologue
2009-11-05 10:13:11 |
Thank you!
|
kiselev
2011-03-18 11:29:03 |
Well done!
|
timmy
2011-05-02 20:51:54 |
this is correct.
also, yosuns solution, as usual is absolutely terrible and makes no sense at all. Honestly who is yosun, and why is all of yosuns solutions so bad???
I mean this site is great, but some of these solutions are just grossly wrong in terms of methodology, even if they are technically correct.
|
timmy
2011-05-02 20:55:15 |
let me elaborate: when I say Yosun's solutions are bad, I don't mean they are wrong, far from it.
The problem is that they go into to much detail and theory to be almost useless to the test taker.
The test-taker needs to UNDERSTAND the basics of what they need to know and QUICKLY SOLVE the problem. Yosun's solution don't EXPLAIN the problem well at all. The solution given above is terrible in terms of explaining what is going on in the problem with the rate and the 1% etc.
|
Quark
2011-10-05 14:32:36 |
yosun created this website so you should actually be thankful for all of his solutions.
|
rizkibizniz
2011-11-07 00:44:57 |
@Quark you mean -her- solutions. Yosun is a she.
|
|  | tensorwhat
2009-03-19 20:39:42 | This is way more simple....
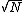 /N = 1% = 1E-2 /N = 1% = 1E-2
 Solve for N Solve for N
 N = 1/1E-4 = 10,000 s N = 1/1E-4 = 10,000 s
 There are 2 counts per second, so 10,000 s/2 = 5,000 s There are 2 counts per second, so 10,000 s/2 = 5,000 s
Done.
AER
2009-04-02 16:14:24 |
Where 2 is still the average of the ten measurements, and each measurement was 1 sec long.
|
ajkp2557
2009-11-07 05:03:37 |
Small typo: 10,000 should be number of counts (unitless), not measured in seconds. Your units will come from the fact that you're dividing by 2 counts / sec.
|
|  | eshaghoulian
2007-09-29 19:34:12 | I think if you piece together everyone's comments, you'll have a final solution. Here is my thought progression:
The number of counts N is 20 for a time T of 10 seconds, giving a rate R of N/T = 2. Here we invoke the 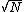 rule without justification, which allows us to say that the uncertainty of an N-count distribution is rule without justification, which allows us to say that the uncertainty of an N-count distribution is 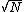 . We use the formula for fractional uncertainty . We use the formula for fractional uncertainty 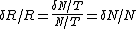 which motivates rampancy's form of the uncertainty. which motivates rampancy's form of the uncertainty.
So, for X seconds, we have a total number of counts 2X, and we use the equation above to get 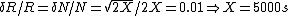
Notice that the fractional uncertainty of the rate is just the fractional uncertainty of the total number of counts. I am not sure about the language here; I want to say that ETS's use of the term "uncertainty" in the question is at best vague, but I am not familiar with this type of experiment (reminiscent of the Q factor, which has as many definitions as it has occurences in physics).
See section "Counting Statistics" in link below for a little more detail
http://www.colorado.edu/physics/phys1140/phys1140_sp05/Experiments/O1Fall04.pdf
ericimo
2007-10-27 14:33:55 |
Correct, except there IS justification.
Since all we know from the problem is that it involves radiation detection, the vague nature allows us to assume that the distribution will follow the most common distribution in radiation detection.
And for most radiation measurements, the distribution is a Poisson distribution (hence Yosun's inclusion of the Poission discussion) which is where the employed rule for uncertainty comes into play.
|
wystra
2016-10-17 04:52:20 |
Best answer
|
|  | michealmas
2006-12-27 19:09:12 | Sorry for the formatting screw-up:
Trying to clear up Yosun's solution - Yosun's formula for uncertainty is wrong. He claims it's:
 /AverageCounts /AverageCounts
when actually it's
 /TotalCounts /TotalCounts
you can correct Yosun's equation by multiplying the denominator by the total seconds, or C as Yosun calls it. That is what he does, though without explanation. |  | michealmas
2006-12-27 19:06:57 | Trying to clear up Yosun's solution - Yosun's formula for uncertainty is wrong. He claims it's:
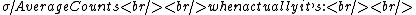 \sigma/TotalCounts \sigma/TotalCounts
you can correct Yosun's equation by multiplying the denominator by the total seconds, or C as Yosun calls it. That is what he does, though without explanation. |  | simpsoxe
2006-11-30 21:43:30 | if you claim that 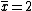 is the average and is the average and 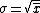 is the standard deviation, then how do you go from there to get that is the standard deviation, then how do you go from there to get that 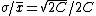 is the answer? I'm confused as to how the C's get in there is the answer? I'm confused as to how the C's get in there |  | rampancy
2006-11-02 00:50:14 | That explanation makes no sense, and seems needlessly complicated.
The total number of counts in 10 seconds is 20. The error in that is Sqrt(20).
Counts = 20 +/- sqrt(20).
The average number of counts is 2, so in N seconds, we should see,
2N +/- sqrt(2N) counts.
We want the fractional error to be .01, so,
sqrt(2N)/(2N) = .01
So N = 5000.
nitin
2006-11-13 14:23:09 |
I agree with rampancy. Yosun, your solution is nonsense, and it seems you don't even know what you're talking about.
|
mr_eggs
2009-08-16 18:21:53 |
You don't have to be a jerk, nitin. This is an open community site to help those trying to get into grad school. If you don't have anything intelligent to add, then fuck off.rnrnA little late.. haha..
|
mr_eggs
2009-08-16 18:31:54 |
You don't have to be a jerk, nitin. This is an open community site to help those trying to get into grad school. If you don't have anything intelligent to add, then fuck off.
A little late.. haha..
|
FutureDrSteve
2011-11-07 14:23:11 |
Also late, but totally agreed. There are still no decent books and few good resources to prepare for the PGRE. This site is an absolute godsend. Yosun's solutions are not always the best solutions for me to have that "Ah ha!" moment, but I imagine that's why she was brilliant enough to make this a community site. And aside from the HATERS, it's a good community. This site is the sole reason I will do well on test day. Thanks, Yosun!
|
wystra
2016-10-17 04:51:25 |
Best answer
|
|  | yosun
2005-11-27 01:50:12 | Poisson Distribution, the way it was meant to be.
Blake7
2007-09-19 06:02:24 |
It's beautiful, Yosun! How can I get a copy of your wonderful book?
|
Ge Yang
2010-10-05 12:46:46 |
Right, Yosun, where can we get your wonderful book?
This website definitely has its own memory...
|
|  |
|
| Post A Comment! |
You are replying to:
I think if you piece together everyone's comments, you'll have a final solution. Here is my thought progression:
The number of counts N is 20 for a time T of 10 seconds, giving a rate R of N/T = 2. Here we invoke the 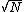 rule without justification, which allows us to say that the uncertainty of an N-count distribution is 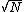 . We use the formula for fractional uncertainty 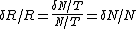 which motivates rampancy's form of the uncertainty.
So, for X seconds, we have a total number of counts 2X, and we use the equation above to get 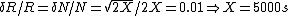
Notice that the fractional uncertainty of the rate is just the fractional uncertainty of the total number of counts. I am not sure about the language here; I want to say that ETS's use of the term "uncertainty" in the question is at best vague, but I am not familiar with this type of experiment (reminiscent of the Q factor, which has as many definitions as it has occurences in physics).
See section "Counting Statistics" in link below for a little more detail
http://www.colorado.edu/physics/phys1140/phys1140_sp05/Experiments/O1Fall04.pdf |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
