|
GR0177 #31
|
|
|
|
|
Alternate Solutions |
FutureDrSteve
2011-11-07 12:22:35 | Oops, this was supposed to be a separate post, not a reply....
If you realize that the ground state energy of positronium is roughly -6.8eV (which I think you have to in order to solve this problem), you don't have to do any math. An electron transitioning down from n=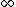 would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). |  |
|
|
Comments |
bill92
2014-10-27 13:17:41 | I just took the exam and there was no positronium question! All my studying was for naught!
Just kidding, I think it went well. Thanks to Yosun for this very helpful site! |  | FutureDrSteve
2011-11-07 12:22:35 | Oops, this was supposed to be a separate post, not a reply....
If you realize that the ground state energy of positronium is roughly -6.8eV (which I think you have to in order to solve this problem), you don't have to do any math. An electron transitioning down from n=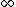 would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). |  | Tommy Koulax
2007-10-31 17:48:57 | Why is the reduced mass m/2 ?
nick1234
2007-11-02 17:16:11 |
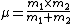
For the hydrogen atom, 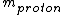 dominates the denominator, and dominates the denominator, and 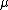 becomes becomes 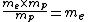
For positronium, 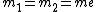 , so , so 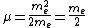
|
|  | rinnie
2007-03-26 21:27:49 | Hydrogen levels E3 - E1 = -1.5 + 13.6 = 12.1/2 = 6.05.
Energy level of positronium is half those of Hydrogen.
FutureDrSteve
2011-11-07 12:20:53 |
If you realize that the ground state energy of positronium is roughly -6.8eV (which I think you have to in order to solve this problem), you don't have to do any math. An electron transitioning down from n=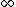 would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A).
|
|  |
|
| Post A Comment! |
You are replying to:
Oops, this was supposed to be a separate post, not a reply....
If you realize that the ground state energy of positronium is roughly -6.8eV (which I think you have to in order to solve this problem), you don't have to do any math. An electron transitioning down from n= 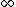 would have initial potential energy of 0, and drop down to final energy -6.8eV, for a max energy change of 6.8eV, eliminating (C), (D), and (E). Since the electron is only falling down from n=3, it stands to reason that the photon would be less energetic than 6.8eV, leaving only answer (A). |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 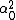 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
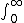 |
| $\partial$ |
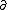 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
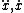 |
| $\sqrt{z}$ |
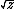 |
| $\langle my \rangle$ |
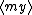 |
| $\left( abacadabra \right)_{me}$ |
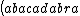_{me}) |
| $\vec{E}$ |
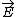 |
| $\frac{a}{b}$ |
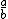 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
