|
GR0177 #40
|
|
|
|
|
Alternate Solutions |
secretempire1
2012-09-04 11:30:01 | One of the good qualitative things to know about inductors is that as soon as a sudden change in current occurs, the inductor acts like an open circuit (no current can flow). But as current stabilizes, the inductor acts like a short circuit (just like a bare piece of wire with negligible resistance).
As soon as the switch is closed, the current attempts to flow through the circuit but is stopped since the inductor looks like an open circuit. Therefore, there is a high voltage on one end, and a low voltage on the other end of the inductor. Right from that statement, we can rule out A, B, and C.
As time goes on, the inductor gradually begins looking more like a piece of bare wire, meaning that it's impedance decreases, resulting in a smaller voltage drop across the inductor.
The "time constant" associated with an LR circuit is equal to L/R. The time constant is a good way to see on what time scale the circuit operates. Therefore, L/R = (10*10^-3)/2 = 1/200 = 5 msec. So choice D is your answer. |  |
|
|
Comments |
Alfred Centauri
2014-10-21 09:04:14 | (1) inductor current through is continuous for finite voltage across: 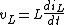
(2) before the switch is closed, the inductor current is 0
Thus, the initial inductor current is  = 0A) and the initial voltage is, by KVL: and the initial voltage is, by KVL:  = 10V - i_L(0) \cdot 2 \Omega = 10V)
Only answers (D) and (E) satisfy the above.
The time constant for a RL circuit is 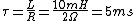 which eliminates (E) leaving (D) as the correct answer. which eliminates (E) leaving (D) as the correct answer. |  | bostroem
2013-01-23 20:06:31 | In the Official solution - how do you solve for V if you don't know I or Q? |  | secretempire1
2012-09-04 11:30:01 | One of the good qualitative things to know about inductors is that as soon as a sudden change in current occurs, the inductor acts like an open circuit (no current can flow). But as current stabilizes, the inductor acts like a short circuit (just like a bare piece of wire with negligible resistance).
As soon as the switch is closed, the current attempts to flow through the circuit but is stopped since the inductor looks like an open circuit. Therefore, there is a high voltage on one end, and a low voltage on the other end of the inductor. Right from that statement, we can rule out A, B, and C.
As time goes on, the inductor gradually begins looking more like a piece of bare wire, meaning that it's impedance decreases, resulting in a smaller voltage drop across the inductor.
The "time constant" associated with an LR circuit is equal to L/R. The time constant is a good way to see on what time scale the circuit operates. Therefore, L/R = (10*10^-3)/2 = 1/200 = 5 msec. So choice D is your answer. |  | walczyk
2011-04-07 08:15:43 | how does one calculate the final voltage? I wish someone had done an exact solution, they are so instructive.
bohrwhore
2013-07-23 21:53:35 |
V(t)=V0*e^(-t*R/L)
|
bohrwhore
2013-07-28 18:50:01 |
woops L/R
|
|  | Imperate
2008-10-06 07:15:15 | One can remember what the time constant is for an R-L circuit by dimensional analysis. Since an R-L circuit contains only these two elements you immediately know the time const mut be a function of R and L. Next V=LdI/dt => [L]=[V][s]/[A]. Secondly the fundamental units of resistance can be obtained from Ohms law [Ohm]=[V]/[A]. As the name suggests the time constant must have units of time! Thus the function of L and R must be rnL/R= [V][s]/[A] *[A]/[V]=[s].rnPlugging this in 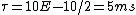 . . |  | scottopoly
2006-11-02 15:19:06 | Well the site seems to be a bit broken and I can't edit my comment, so here goes:
I misread "200s" as "200ms" at first, and so was confused by the "decreases rather quickly".
But really once you realize that these values for the components in this problem are rather standard values that you find in lab, a little experience will tell you that indeed, there is hardly a circuit that moves in 200s time.
sorry about that.
buaasyh
2015-08-26 12:13:11 |
That\'s right. So it is not necessary to really solve the differential equation U=L dI/dt, where I=(10V-U)/2 to get U=10 e^(-2/L t), thus at t= L/2, the voltage U drops by 1/e which is approximately one half.
|
|  | scottopoly
2006-10-29 22:47:24 | Furthemore, I might add that "decreases rather quickly" is, ah, crap. The numers are arbitrary, there is no basis to say anything is "fast". It decrases the rate 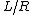 , as Void said, which is neither fast nor slow. , as Void said, which is neither fast nor slow.
Richard
2007-10-25 15:55:55 |
nice... (笑)
|
wangjj0120
2008-10-27 02:21:55 |
HAHA~
It's funny to see a chinese word here.
這個網站很棒 謝謝你~Yosun
|
mpdude8
2012-04-20 21:05:21 |
True, but the GRE is not going to contain examples that aren't physically relevant. A circuit that still has significant voltage after 200 seconds isn't exactly a physically common system.
|
dipanshugupta
2017-03-30 17:10:35 |
भाई चाइनीज़ मैं क्युन बात कर रहे हो?
|
|  | Void
2005-11-11 08:58:21 | To see why (D) is right, recall that the time constant for an RL circuit is given by 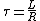 . Inputting the values makes (D) the "obvious" choice. . Inputting the values makes (D) the "obvious" choice. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
