|
GR0177 #69
|
|
|
|
|
Alternate Solutions |
atomike238
2011-03-10 12:50:58 | Assuming the boundaries are vacuum-oil, oil-glass, then there will be a phase shift at the vacuum-oil boundary since 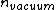 < < 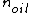 and another phase shift at the oil-glass boundary because and another phase shift at the oil-glass boundary because 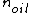 < < 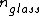 . .
That tell us that constructive interference happens for integer wavelengths (m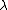 ). ).
Light crosses a distance d in t=d/c. but since its speed is lower in oil, 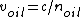 . Then t=d/v=nd/c. Its as if light had to travel nd instead of d. . Then t=d/v=nd/c. Its as if light had to travel nd instead of d.
Therefore the condition for constructive interference becomes
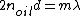
The next minimum thickness other than zero is when m=1.
So 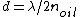 = 200nm = 200nm |  | ee7klt
2005-11-11 04:25:27 | Hi,
I think E123 has got it right and just wanted to add my 2 cents to this to see if this reasoning is right.
I think the quantity of interest is the optical path length (OPL) where 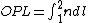 since this is really the distance that the light 'sees'? since this is really the distance that the light 'sees'?
Thus for first order constructive interefence at the air/oil boundary, we require 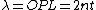 giving giving 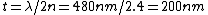 . .
|  |
|
|
Comments |
kaic
2013-10-15 23:14:18 | I don't know if I'm completely misunderstanding this problem or what, but it seems to me that when the wave which reflects off the glass re-emerges, it should be 180 degrees out of phase with the wave which reflected off the oil.
We have a wave incident on a surface of higher index of refraction than air. Part of it reflects with a phase change of 180 degree, part of it is transmitted, also with a phase change of 180 degrees.
The portion which is transmitted then reflects off of the glass, again undergoing a 180 degree phase change, making it back in phase with the initial incoming wave, and now 180 degrees or 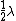 out of phase with the first reflected wave. out of phase with the first reflected wave.
In which case shouldn't we want the path length difference 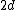 to be equal to half a wavelength (in medium) so that overall the second reflected wave is 180 degrees out of phase with the incident wave, and in phase with the first reflected wave? to be equal to half a wavelength (in medium) so that overall the second reflected wave is 180 degrees out of phase with the incident wave, and in phase with the first reflected wave?
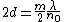 for odd for odd 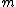
kaic
2013-10-15 23:19:18 |
Apparently I've been working under the false assumption that the transmitted wave also undergoes a phase change, which is apparently not true.
|
|  | Jovensky
2013-04-11 21:21:35 | I don't know why we can assume that it is air/vacuum above the oil. |  | risyou
2012-11-07 21:01:01 | I thought with the light distance in oil is l'= n d (n, d: index and thinness of the oil)
And for the reflected point, which is the lightest (m)λ=2l' where m = 1. You could got the exactly 200 |  | johnhero2010
2012-10-20 04:03:08 | why did u use the destructive interference formula, while here we have a constructive one because the 1st ray reflected from the oil surface and also the 2nd ray reflected from the glass surface,both have a 180 degree change in phase so they actually are in phase so constructive interference formula should be used, but the problem is that the answer is 100 nm which is not in the answer choices..so what is wrong?rn
cz
2012-11-04 22:10:18 |
I believe all your issues have been corrected in the solution. The formula used is for constructive interference. and the answer should be 200nm.
|
|  | atomike238
2011-03-10 12:50:58 | Assuming the boundaries are vacuum-oil, oil-glass, then there will be a phase shift at the vacuum-oil boundary since 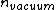 < < 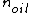 and another phase shift at the oil-glass boundary because and another phase shift at the oil-glass boundary because 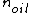 < < 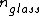 . .
That tell us that constructive interference happens for integer wavelengths (m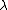 ). ).
Light crosses a distance d in t=d/c. but since its speed is lower in oil, 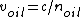 . Then t=d/v=nd/c. Its as if light had to travel nd instead of d. . Then t=d/v=nd/c. Its as if light had to travel nd instead of d.
Therefore the condition for constructive interference becomes
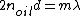
The next minimum thickness other than zero is when m=1.
So 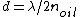 = 200nm = 200nm |  | Kabuto Yakushi
2010-09-11 09:27:02 | I think it's important to note that the question only asks about the reflection off the thin film of oil. This makes for constructive interference because:
the phase change of the reflected light entering the oil from the air is 180 degrees
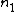 < < 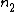 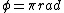
the phase change for the reflected light entering the glass from the oil is 180 degrees.
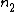 < < 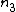 , , 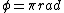
both wave are out of phase by 180 degrees constructive interference occurs. We use the constructive interference formula for thin lenses:
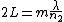
We have to be careful because if the question had asked about the entire oil/lens system than we would have had partially constructive interference. The light reflected off of the back of the glass (if the back of the glass is exposed to air that is) would have a 0 degree phase change and would destructively interfere with the reflected light from the front of the glass.
For more on this topic refer to Halliday and Resnick Fundamentals of Physics chapter 35-7 which has a fairly concise treatment of thin film interference. |  | CaspianXI
2009-03-01 19:22:35 | This is minor... but the solution said that 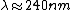 . I think the author meant . I think the author meant 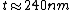 . . |  | Poop Loops
2008-11-01 20:29:01 | Okay, so what does the glass have to do with it? Do we just ignore it or what?
gamercora
2010-09-07 09:15:25 |
the index of refraction of glass is bigger than that of oil. it means there is a half-wave loss. but there is also a half-wave loss between air and oil so no loss of course.
|
|  | etano
2007-11-02 10:15:13 | http://physics.bu.edu/~duffy/PY106/Diffraction.htmlrnthis helped me.
etano
2007-11-02 10:15:49 |
http://physics.bu.edu/~duffy/PY106/Diffraction.html
|
|  | irishroogie
2007-10-02 14:15:17 | But I thought the formula for constructive interference in thin films was: 2nt = (m+1/2)*lambda, m=0,1,2... and m=0 for minimum thickness.
Using that formula you get 100nm which is clearly none of the answers, but I am confused as to where I am going wrong?
irishroogie
2007-10-02 20:44:06 |
Kk, So my question was flawed. 2nt=m*lambda is correct since the phase changes again by 180 at the oil glass interface. Woops!
|
|  | ee7klt
2005-11-11 04:25:27 | Hi,
I think E123 has got it right and just wanted to add my 2 cents to this to see if this reasoning is right.
I think the quantity of interest is the optical path length (OPL) where 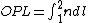 since this is really the distance that the light 'sees'? since this is really the distance that the light 'sees'?
Thus for first order constructive interefence at the air/oil boundary, we require 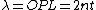 giving giving 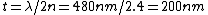 . .
|  | E123
2005-11-09 14:52:08 | i think the 200nm instead of 240nm is because of the 1.2 refractive index --> lambda(oil) = lambda(air) / 1.2
yosun
2005-11-09 15:29:14 |
E123: thanks for the better approximation; it has been added.
|
f4hy
2009-04-02 17:33:39 |
also it is important to note that the index of refraction of glass is > than that of oil. Otherwise on the reflection there would have been a phase shift of 
|
|  |
|
| Post A Comment! |
You are replying to:
I don't know if I'm completely misunderstanding this problem or what, but it seems to me that when the wave which reflects off the glass re-emerges, it should be 180 degrees out of phase with the wave which reflected off the oil.
We have a wave incident on a surface of higher index of refraction than air. Part of it reflects with a phase change of 180 degree, part of it is transmitted, also with a phase change of 180 degrees.
The portion which is transmitted then reflects off of the glass, again undergoing a 180 degree phase change, making it back in phase with the initial incoming wave, and now 180 degrees or 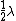 out of phase with the first reflected wave.
In which case shouldn't we want the path length difference 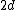 to be equal to half a wavelength (in medium) so that overall the second reflected wave is 180 degrees out of phase with the incident wave, and in phase with the first reflected wave?
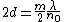 for odd 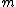 |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 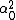 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
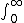 |
| $\partial$ |
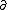 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
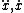 |
| $\sqrt{z}$ |
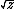 |
| $\langle my \rangle$ |
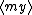 |
| $\left( abacadabra \right)_{me}$ |
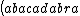_{me}) |
| $\vec{E}$ |
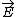 |
| $\frac{a}{b}$ |
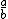 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
