|
GR0177 #73
|
|
|
|
|
Alternate Solutions |
ilikefluids
2017-07-09 15:44:05 | 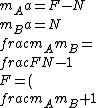N \\\\ \\\\ \\textrm{All of these quantities are easy to calculate;} \\\\ \\frac{m_A}{m_B}=16/4=4, \\\\\\mu N = m_B g \\Rightarrow N = \\frac{m_B g}{\\mu} = \\frac{(4)(10)}{0.5} = 80 \\\\ \\textrm{Hence, }F = 5(80) = 400, \\textrm{ choice (D)}) |  | R0BB23
2008-06-30 08:46:19 | 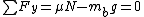
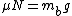
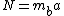
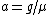
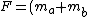a)
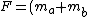g/\mu) |  |
|
|
Comments |
ilikefluids
2017-07-09 15:44:05 | 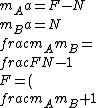N \\\\ \\\\ \\textrm{All of these quantities are easy to calculate;} \\\\ \\frac{m_A}{m_B}=16/4=4, \\\\\\mu N = m_B g \\Rightarrow N = \\frac{m_B g}{\\mu} = \\frac{(4)(10)}{0.5} = 80 \\\\ \\textrm{Hence, }F = 5(80) = 400, \\textrm{ choice (D)}) |  | asdfuogh
2011-11-09 18:09:11 | So, you can figure out the normal force pretty quickly to be 80 N. Then you flip your head around and imagine the second block to be accelerated by the normal force due to the first block, which would give the acceleration to be 80N/4 kg = 20 m/s^2. Then you realize that the blocks are moving at the acceleration because there is a normal force between them, so the whole force on the system is a*total_mass = 20 m/s^2 * 20 kg = 400 N.
:( Too bad this isn't the kind of stuff you can come up with under pressure... I kept messing up the calculations when I was doing this as a practice test :(. |  | Dodobird
2010-11-01 08:50:49 | Use the principle of equivalence. Coefficient of static friction gives us one part of vertical force for every two parts of horizontal force. We need 40 N of vertical force, therefore we need 80 N of horizontal force on B. Because we have to push the entire system, we need five times this force, which is 400 N. Answer = D |  | carl_the_sagan
2008-11-07 22:05:17 | I'm not sure if this is a valid way to tackle the problem but it's how my messed up line of thinking went:
The block B needs to be pushed up equal to the force gravity exerts on it to stay in place. Take gravity to be 10m/s^2 for convenience and it needs 40N.
However, the coefficient of friction is only .5, so you have to push twice as hard, so 80N. This means you need to accelerate B by 80N/4kg = 20m/s^2 horizontally to produce enough "lift" to balance things. Since the entire system is 20kg, F = 20kg*20m/s^2 = 400N
bert
2009-11-06 11:15:06 |
I like this solution. These problems should be solved with quick logic, not tedious math and equations whenever possible. :)
|
solidstate
2011-11-04 22:05:52 |
This works pretty fine.
|
|  | R0BB23
2008-06-30 08:46:19 | 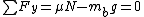
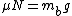
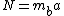
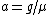
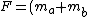a)
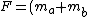g/\mu)
N
2011-04-07 20:55:31 |
To clarify RoBB23's solution: the important point to recognize here is that the horizontal force on the two blocks is not the same, but that they accelerate at the same rate: 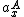 = = 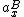 . Then it's just the normal stuff. . Then it's just the normal stuff.
|
John777
2011-11-07 10:45:40 |
Good Job!
|
QuantumCat
2014-09-22 17:19:18 |
Fast and efficient. Love it!
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
