|
GR0177 #87
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
dinoco
2010-11-13 10:57:39 | 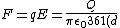^2}) should be should be 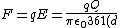^2}) |  | alpha137
2007-11-02 18:06:06 | Just wanted to alert you to the following typo:
E-field equation contains a superfluous 4 in the numerator (i.e. 4Q). Love the site by the way!
geof
2008-10-30 17:12:11 |
no, actually the 4 comes from r^2
r=19d/2
therefore, r^2 = (361/4)*d^2
this 4 cancels out with the 4 in the denominator and thus the above solution is correct
|
|  | ee7klt
2005-11-11 04:31:26 | Hi,
Just wondering, why is the potential constant at all points ( I can see why it would be at the center).
I guess one can also get a zero E field inside by Gauss' Law: any gaussian surface does not enclose charge, and thus 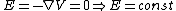 . .
Jeremy
2007-10-25 14:02:06 |
Just considering the sphere on the left...
Gauss's law alone does not say the field inside is zero. This is a common mistake that I used to make a lot. 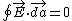 does not mean does not mean 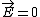 . It's easy to spot a counterexample in the differential counterpart . It's easy to spot a counterexample in the differential counterpart 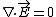 . Here, you see that the most general solution is that . Here, you see that the most general solution is that  is the curl of a vector. Even if you consider is the curl of a vector. Even if you consider 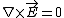 , both equations would hold (be identically zero) were , both equations would hold (be identically zero) were  to be any constant vector, e.g. to be any constant vector, e.g. 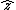 . .
The easiest way to see why 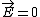 for all points inside the sphere is to consider a rotation of the sphere about an axis passing through the sphere's center and a point that you want to know for all points inside the sphere is to consider a rotation of the sphere about an axis passing through the sphere's center and a point that you want to know  at. This rotation leaves the charge distribution unaltered, but would rotate any non-radial component at. This rotation leaves the charge distribution unaltered, but would rotate any non-radial component  might happen to have. This would be nonsense though because the charge distribution hasn't changed. ( might happen to have. This would be nonsense though because the charge distribution hasn't changed. ( cannot have two directions at the same point in space.) After this consideration, it is only possible for cannot have two directions at the same point in space.) After this consideration, it is only possible for  to have a radial component, but this component must be zero for Gauss's law to hold. Thus, to have a radial component, but this component must be zero for Gauss's law to hold. Thus, 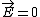 everywhere inside the sphere. everywhere inside the sphere.
|
Poop Loops
2008-11-02 00:28:09 |
That's too long. Here's a simpler explanation:
At the center it's easier to understand and see that all the charges on the shell exhibit the same force on the one in the center, but in different directions, so the net force is 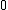 . .
When you move away from the center, what happens is you get closer to some charges, so they exhibit a stronger force. You also get further away from other charges, so they exhibit a lower force.
However, there is *more* charge exhibiting a force now. Think about it. If you get really close to the shell wall, only a few charges are pushing you to the center and essentially the rest of the shell is "behind" you pushing you forward. And it just so happens that the amount of charge grows at the same rate as the strength of the force, i.e. 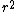 , where , where 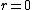 at the center. at the center.
Okay, so that's just as long, but mine doesn't have as much math. :)
|
wittensdog
2009-09-24 20:40:58 |
The simplest explanation, and the best way to make sure you have it all straight, in my opinion, is to notice the part about UNIFORM distribution of charge on the SPHERE. Because of this total symmetry, if you put a tiny test charge on the surface, it would have no preference in which direction to move, in other words, the surface has constant potential.
A potential distribution is always specified by its value on the boundary. When you have a CONSTANT potential on ANY boundary, it must be the same constant potential inside, since there can only be one solution to Laplace's equation, and this is it. This means there is no field inside, and in combination with the superposition of electric potentials, you know the only thing to consider is the other sphere.
(Sorry about the caps - I'm not trying to be offensive, I'm just too lazy to look up how to do italics)
If this were a conductor, the ability of the electrons in the metal to freely move would allow them to automatically assume whatever distribution gives them a constant potential over the surface, since this is energetically favored, and hence a conductor never has a field inside. But of course we have insulators in this problem, and the uniform distribution needs to be set up that way.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
