|
GR8677 #15
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ernest21
2019-08-10 03:09:28 | A great day and a very explicit information. apex hq |  | fredluis
2019-08-08 13:02:41 | The writing style is somewhat conversational and straightforward, and the problems show a nice range of difficulty. tile contractor |  | joshuaprice153
2019-08-08 07:04:25 | I was suggested this blog by means of my bro. I am not sure whether or not this publish is written by means of him as no one else understand such precise about my problem. You’re wonderful! Thanks! towing service |  | yosun2015tester
2015-07-22 12:26:56 | what |  | yosun2015tester
2015-07-22 12:25:20 | testing123 july 22 2015 |  | mpdude8
2012-04-15 20:09:22 | For this, I just looked at it logically. Think about N = a small number, like 2. A and E are out -- there's always at least a chance that neither one will be in that subset, or one of them will. Also, when N = 2, the probability that both particles are outside of such a small subset of the total volume should be almost 1. B is out, as even for N = 2, the probability is extremely small, and races towards zero as you increase N slightly.
D is also out, as it is the exact opposite effect of what you want, logically. Probability, as you add more particles, should tend to 0. C is the only choice that has the correct tendency as N grows, and at a reasonable rate of increase. |  | livieratos
2011-11-07 03:54:30 | so the probability of one atom to be in the given small volume is the ratio of the small volume to the entire volume? P(yes) = 1E-6/1 = 1E-6?
Ajith
2015-10-14 09:30:40 |
I guess =\\frac{No. of atoms in that volume}{tolal number of atoms}) \r\nHere, No. of atoms in \r\nHere, No. of atoms in 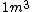 = N\r\nNo. of atoms in = N\r\nNo. of atoms in 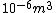 = No. of atoms in = No. of atoms in 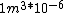 = =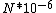 \r\nThus, \r\nThus, =\\frac{N*10^{-6}}{N}) = =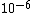
|
|  | ubaraj
2007-11-01 01:15:13 | the volume is 1. There can be no He atoms in the volume 10E-6. So all N atoms have to be within the volume (1-10E-6), and so the probability becomes (1-10E-6)^N. The choice is C!! |  | Furious
2007-08-17 15:40:58 | You really just need to look at the limiting factors in this problem.
When N is 0 the probability should be 1. That eliminates A and D.
When N is extremely high, the probability should go to 0. That eliminates E, (not that any of us thought it was E)
So that leaves us with B and C. Which both match the limiting cases, but just think about it when N is 1. When N is one there should be a very high chance that it is not in the specific 1e-6 area.
For B, the probability is 1e-6, not very high at all.
For C, the probability is 0.99999, pretty close to 1.
This helped me since, I get super confused whenever I think about probability. |  | wishIwasaphysicist
2006-01-24 11:27:10 | How did you connect P(Ngasatoms) = (1-1E-6)^N to answer C?
yosun
2006-02-01 22:02:05 |
hi wishIwasaphysicist, because each of the N molecules are independent, the probability would be multiplicative. Thus, if the particle for each particle is P, the probability for N particles would be 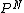 . .
|
yosun2015tester
2015-07-22 12:31:28 |
testing123
|
yosun2015tester
2015-07-22 12:37:21 |
testering12345
|
yosun2015tester
2015-07-22 12:49:08 |
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
