|
GR8677 #20
|
|
|
Problem
|
|
 |
Special Relativity }Rest Energy }Rest Energy
If one remembers the formulae from special relativity, arithmetic would be the hardest part of the problem.
The problem is to solve 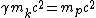 , where , where 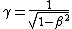 and and 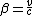 . .
The rest-mass of both the kaon and the proton are given in the problem. Thus, the equation reduces to 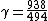 . .
Now, because the range of velocities vary significantly between 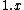 and and 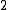 , one can't directly approximate that as 2. Boo. So, long-division by hand yields approximately , one can't directly approximate that as 2. Boo. So, long-division by hand yields approximately 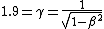 . .
The author of this site prefers to use fractions instead of decimals. Thus 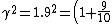^2= 1+\frac{81}{100} +\frac{180}{100} =\frac{262}{100}) . Express . Express  in terms of in terms of 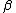 to get to get 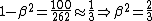 . .
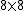 is about 64, so the velocity has to be greater than 0.8c. The only choice left is (E). is about 64, so the velocity has to be greater than 0.8c. The only choice left is (E).
If one has the time, one might want to memorize the following:
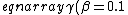&=&1.005\\
\gamma(\beta=0.25)&=&1.033\\
\gamma(\beta=0.5)&=&1.155\\
\gamma(\beta=0.75)&=&1.51\\
\gamma(\beta=0.9)&=&2.29<br />
\end{eqnarray})
, or perhaps a more elaborate list of 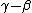 correlations. correlations.
If one knew that before-hand, then one would immediately arrive at choice (E).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ernest21
2019-08-10 03:09:34 | Its a good approach to solve problems @ home,interesting. wolfgang krauser |  | fredluis
2019-08-09 04:13:03 | Both get me closer to 2 compared to the other given answers, but nothing I can think of can give me an exact answer of two. As for the answer explanation here, I am just fairly uncomfortable with the idea that adding two different units together can get the correct answer. tree removal |  | joshuaprice153
2019-08-08 07:33:21 | Pretty insightful post. Never thought that it was this simple after all. I had spent a good deal of my time looking for someone to explain this subject clearly and you’re the only one that ever did that. Keep it up. house painting |  | JoshWasHere
2014-08-20 08:12:31 | In working this out, I approximated 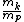 = = 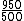 =1.9 which makes it easier to work with. Then in working out the algebra, I approximated =1.9 which makes it easier to work with. Then in working out the algebra, I approximated 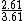 = = 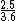 which made taking the square root extremely simple. which made taking the square root extremely simple. 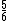 is nearly .85 c so without too many assumptions or generous approximations, I got nearly the right answer in a short amount of time. is nearly .85 c so without too many assumptions or generous approximations, I got nearly the right answer in a short amount of time. |  | dak213
2014-06-30 17:58:42 | I think they forgot to add the 1 in the 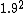 equation. I got equation. I got 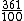 then solving for then solving for 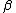 I got exactly 0.85c I got exactly 0.85c  E E
dak213
2014-06-30 18:00:13 |
Ah, I see this issue has been addressed. I should have read the comments at the bottom.
|
|  | deniskrasnov
2013-01-19 00:08:42 | i have a suspicion that ETS only wants you to remember Pythagorean triple 3:4:5
wich translates into:
beta = 0.8 => gamma = 5/3 = 1.66...
beta = 0.6 => gamma = 5/4 = 1.25
and thus, dealing with similar problem one should first check if one of these is enough to identify the correct answer quickly
the first one is sufficient in this case
gamma = 938/494 > 850/500 > 1.7 > 1.66.. => beta > 0.8 |  | oliTUTilo
2012-11-01 16:43:56 | If we algebraically solve for v (or 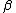 ) instead of ) instead of  , as Yosun does, it seems easier to approximate the answer. , as Yosun does, it seems easier to approximate the answer.
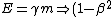}^{-\frac{1}{2}} = \frac{E}{m} \Rightarrow \beta = {(1-{(\frac{m}{E})}^2)}^{-\frac{1}{2}})
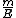 is approximately is approximately 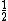 , so , so 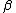 is approximately is approximately }^{-\frac{1}{2}}) , which is 1.7 something divided by 2, or approximately 0.85. v is , which is 1.7 something divided by 2, or approximately 0.85. v is 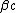 , so badabingbadaboom. , so badabingbadaboom.
In general, I'd algebraically solve for the variable in question first, gaining the greatest transparency, but redmomatt's method is even a bit faster here.
|  | redmomatt
2011-10-14 08:59:20 | Why can't we do this....?
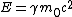
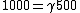
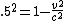
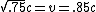  (E) (E) |  | checkyoself
2011-10-05 10:46:45 | Approximating 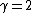 is fine. You end up with is fine. You end up with 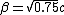 which you know must be greater than 0.75c so the answer must be E. which you know must be greater than 0.75c so the answer must be E. |  | archard
2010-05-25 18:33:08 | Instead of doing the long division by hand, you could just say that gamma is less than 2. Solving the inequality you get that v > 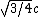 . E is the only answer that satisfies this. . E is the only answer that satisfies this.
Crand0r
2010-11-12 08:49:13 |
Actually, you should get that 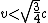 . All of the answers satisfy this, but you also know that . All of the answers satisfy this, but you also know that 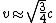 , which leaves only E. , which leaves only E.
|
|  | lamejiaa
2009-08-30 09:09:49 | The result is good but (19/10)(19/10) = 361/100
walczyk
2011-04-06 17:37:34 |
^^this is true. you can check this quickly by 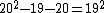 . After a couple steps you will end up with . After a couple steps you will end up with 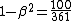 . Do a little math and you'll get . Do a little math and you'll get 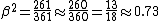 Phew, all these relativistic problems really have you scratching away with your pencil, but the most time consuming part of this problem will be the long division, good luckk. Phew, all these relativistic problems really have you scratching away with your pencil, but the most time consuming part of this problem will be the long division, good luckk.
|
|  | jmason86
2009-08-16 16:22:01 | If you DO use 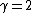 then you get roughly then you get roughly 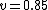 . Not bad, I say. If the listed velocities were closer together, we might have a problem but they are pretty well spaced. Since it takes about 20 seconds to solve through with . Not bad, I say. If the listed velocities were closer together, we might have a problem but they are pretty well spaced. Since it takes about 20 seconds to solve through with 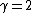 , I suggest using this, and if the answer came out too far from those listed, to go back and solve for 1.x. If you did have to do this, at least you already solved for v and you could just plug back in without deriving it again. , I suggest using this, and if the answer came out too far from those listed, to go back and solve for 1.x. If you did have to do this, at least you already solved for v and you could just plug back in without deriving it again.
wittensdog
2009-09-25 17:26:02 |
I strongly agree - whenever you see spaced out answers, that's always your clue to approximate.
One thing I always remember is that when gamma is 2, the speed is sqrt(3)/2 , which is something like 0.866 or something like that. A value of 2 for gamma comes up in a lot of places, such as when rest energy and kinetic energy are equal, so it's a good thing to remember. Seeing that the ratio is almost two, that the answers are well spaced, and that there's something in the ball park of 86% of c, you should immediately go for it.
Seriously, NEVER do math if you see spaced out answers. One big example I can think of is the drift velocity problem, where each of the answers were spaced out by like 7 orders of magnitude. There was a factor of 1.6(pi) or something like that, but that's certainly not enough to swing 7 OM! Of course it's not quite as dramatic here, but still, no one wants to do long division on the physics GRE.
|
|  | nz_gre
2007-09-24 18:12:08 | why are we neglecting the fact that
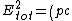^{2} + m_{0}c^{2})
And then finding the momentum  velocity? velocity?
Surely, if the total kaon energy is equal to the proton rest mass then
938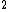 = (pc) = (pc)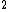 + (494) + (494)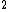 and we go from there? and we go from there?
bkardon
2007-10-05 13:31:04 |
The expression for 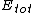 is in fact equivalent to the expresssion is in fact equivalent to the expresssion
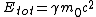
as follows (here 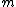 is relativistic mass, is relativistic mass, 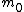 is rest mass) is rest mass)
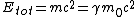
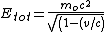^2)})
^2) = m^2_0 c^4)
^2 = m^2_0 c^4)
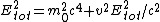
Here I will use 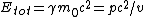
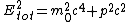
QED
|
FutureDrSteve
2011-10-29 13:44:19 |
Another consideration with your approach is that you still need to calculate 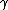 because once you get down to because once you get down to
^2 = 7.5 E5)
in order to solve for v, you need to use:
p = 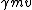
Since you need the other approach to solve for  , you might as well stick with that method to save time and effort , you might as well stick with that method to save time and effort
|
FutureDrSteve
2011-10-29 13:56:04 |
Correction: You don't NEED to solve for  using the other method. You can use the definition of using the other method. You can use the definition of  to solve for v, but using the simpler approach will reduce the risk of making a careless mistake, plus you will save lots of time, which, as far as I'm concerned, is the cardinal rule of the PGRE. to solve for v, but using the simpler approach will reduce the risk of making a careless mistake, plus you will save lots of time, which, as far as I'm concerned, is the cardinal rule of the PGRE.
|
ryanjsfx
2014-10-20 11:32:20 |
I thought using 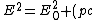^{2}) wasn't so bad. Observe (with c set to 1):rnrn wasn't so bad. Observe (with c set to 1):rnrn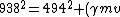^2 )
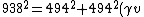^{2} )
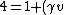^{2} )
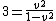
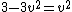
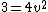
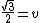
 is about 1.7 and 1.7 divided by 2 is about 0.84 is about 1.7 and 1.7 divided by 2 is about 0.84
Done!
|
|  | leftynm
2006-10-30 17:05:27 | This is much simpler than that.
Once you have gamma*m_k = m_p, plug in gamma = [1-(v/c)^2)]^-1, and solve for v/c. You get v/c = sqrt(1 - (m_k/m_p)^2). If you allow m_k/m_p = 1/2, which it just about is, then you get v/c = sqrt(3)/2. From seeing this so much in trig, I know sqrt(3)/2 = 0.866. Then v/c is about 0.866c. So choice E is very close.
blah22
2008-03-22 13:10:35 |
How is that not, basically, what she did? Just in more detail.
|
|  | radicaltyro
2006-10-21 12:59:15 | 1.9^2 = 3.61 = 361/100, not 262/100
achca
2012-06-26 03:55:13 |
absolutely right!
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
