|
GR8677 #21
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
fredluis
2019-08-09 04:15:41 | In general, I\'d algebraically solve for the variable in question first, gaining the greatest transparency, but redmomatt\'s method is even a bit faster here. pressure cleaning |  | joshuaprice153
2019-08-08 07:35:26 | I\'ll try to return back With A Completely different browser to check out Things! Also, I put a link to your blog at my site, hope you do not mind? towing service |  | blacksheep
2017-09-20 11:36:53 | Although this site doesn\'t see a lot of activity any more, maybe someone will see my question: every source I consult says the space-time interval is (delta-s)^2, NOT delta-s. Yet clearly it\'s the latter quantity ETS is after here. It\'s not a problem with respect to answering the question, since \"4\" is not among the answer choices, but what gives?
misael24
2017-10-19 07:04:11 |
Hello, yeah not many people are using this site but it is proving to be very helpful in studying for the GRE.\r\n\r\n Everywhere that I look I seem to find s^2 = [delta r]^2 - c^2[delta t]^2. I did find other notations but the other was simply s = [r^2 -(c^2)(t^2)]^(1/2).\r\n
|
|  | mpdude8
2012-04-15 20:29:10 | As the original poster points out, this boils down to finding the distance between two points (sqrt((x1 - x2)^2 + (y1-y2)^2 + (z1-z2)^2) - (t1-t2)^2). The only part is remembering to subtract the change in time, rather than add. |  | FortranMan
2008-10-17 13:28:48 | So this is all about how the interval ds is invariant because c is the same in all inertial systems in relative motion, right? So the relations are given as follows.
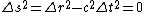
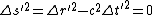
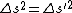
So how on Earth do you manage to get rid of the 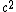 ? I've tried redefining dt as ? I've tried redefining dt as
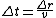
or using the length contraction eq.
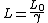
Both get me closer to 2 compared to the other given answers, but nothing I can think of can give me an exact answer of two. As for the answer explanation here, I am just fairly uncomfortable with the idea that adding two different units together can get the correct answer.
mangree
2008-10-18 07:03:30 |
The problem tells you to use units such that the speed of light is 1.This is how you "get rid" of c^2 (couldn't manage the syntax for that).
As for the different units,if c=1 then (m/s)=1  m=s m=s
|
|  | rajsareen
2006-12-01 04:32:27 | If you use the equation for the interval in paranthesis (equivalenty ... ) you get -4, upon which the length becomes imaginary. Maybe only the first equation is appropriate?
VanishingHitchwriter
2006-12-01 14:01:01 |
Note that imaginary numbers are just another tool to use when doing relativity calculations. You can either use a metric or use imaginary numbers. Both views are valid.
|
|  | dicerandom
2006-09-09 12:06:07 | The other thing you need to recall in order to do this problem quickly is that the spacetime interval between two events is invariant, i.e. it does not depend on the reference frame. By asking what the interval is in the O' frame I think the problem is trying to trick you into transforming the events into that frame before calculating the interval.
bkardon
2007-10-05 13:56:18 |
I agree, although one should arrive at the correct answer after Lorentz-transforming the events, it would just be a big waste of time. Which is just the kind of evil trick ETS likes.
|
lattes
2008-10-13 08:11:29 |
agree with both of you. The key fact here is to remember that space-time intervals are invariant.
|
alemsalem
2010-09-20 06:26:00 |
the key fact is that ETS likes evil tricks :)
|
neon37
2010-11-01 08:52:54 |
I dont think this is an evil trick, on the contrary, it is a fundamental concept that the metric is invariant for all inertial reference frames.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
