|
GR8677 #22
|
|
|
Problem
|
|
 |
Electromagnetism }Lorentz Transformation
When an electric field is Lorentz-transformed, afterwards, there might be both a magnetic and electric field (in transverse components). Or, more rigorously, one has,
\\
E_z'&=& \gamma(E_z+vB_y)\\
B_x' &=& B_x\\
B_y' &=& \gamma(B_y + E_z v/c^2)\\
B_z' &=& \gamma(B_z-vE_y/c^2),<br />
\end{eqnarray})
for motion in the  direction.
(A) Obviously not. Suppose initially, one has just 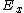 , afterwards, there's still  .
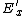(B) True, as can be seen from the equations above.
(C) Not true in general. Suppose  . Afterwards, the transverse components are off by a  even if there's no B field to start with.
(D) Nope.
(E) Mmmm... no need for gauge transformations.
|
|
|
Comments |
casseverhart13
2019-09-26 03:29:58 | Hi,I just discovered your problem.... car window tinting
danielsw98667
2019-10-21 07:23:51 |
Obviously, the answer is A if we will apply the principle of Special Relativity - Electromagnetic Field. random numbers generator
|
|  | fredluis
2019-08-09 04:20:09 | I believe Jeremy ans was better. In the copper there is no significant gain in number of conductive electron but decrease in their sweeping velocity because of the impurities seen as obstacles. pressure cleaning |  | joshuaprice153
2019-08-08 07:37:32 | Hey, would you mind if I share your blog with my twitter group? There’s a lot of folks that I think would enjoy your content. Please let me know. Thank you. towing service | | djh101
2014-08-27 16:38:09 | You can eliminate almost all of the answers without really knowing anything about relativity.
A. Assume observer 1 = observer 2. According to this, an identity transformation will transform an electric field into a magnetic field.
C. From basic E&M, you should know that there's a little bit of symmetry going on between electricity and magnetism. With only that in mind, you can eliminate both C and D. They can't both be true, so by symmetry, neither is true.
D. See above. | | wittensdog
2009-09-25 17:53:58 | In general, what happens is that the field tensor transforms with two factors of whatever matrix corresponds to the given Lorentz transformation. The conditions on the matrices that are in the Lorentz group are not terribly strict, and certainly we know from the simple case of a boost along the x-axis that the components can mix into each other (think about the usual space and time four-vector, and how it transforms).
In general, for a Lorentz transformation, whatever four-vector or tensor you have can have its components mix together pretty generally.
Also, at least in the classical realm, fields NEVER depend on gauge in any way. The issue of gauge fixing only ever comes up when you start working with potentials, which are not measurable. So immediately throw out anything involving gauge dependence when asked about fields. | | FortranMan
2008-10-17 23:15:56 | For more on this topic, look around for Relativistic Electrodynamics, specifically in Griffiths section 12.3. Imagine the case of a large parallel-plate capacitor moving perpendicular to their surface areas, and imagine what the Lorentz contraction does to the charge distributions on the plates. This ends up increasing the electric field that's perpendicular to the direction of motion. Note for a parallel-plate capacitor situated such their motion is parallel to their surfaces, this contraction does not occur and the field remains unchanged. | | grae313
2007-10-07 15:50:57 | On choice (E), does the Lorentz transformation already assume the Lorentz guage?
rorytheherb
2008-10-06 10:22:16 |
yeah I'm looking at griffiths EM and it's not really illuminating this particular question. i knew of course that E and B mix in S.T.R., but when I saw choice E, I recalled the Lorentz gauge and got duped. Can anyone clarify why how we can say E and B mix _without_ first specifying a gauge?
|
dean
2008-10-09 21:00:55 |
I'm not sure there's any relevance at all. Gauge transformations talk about potentials, not fields. A (the vector potential) may change depending on what gauge you're using, but B does not, and can not, else we'd have a physically different situation. Lorentz transformations talk about fields directly in different inertial frames.
|
| |
|
| Post A Comment! |
You are replying to:
In general, what happens is that the field tensor transforms with two factors of whatever matrix corresponds to the given Lorentz transformation. The conditions on the matrices that are in the Lorentz group are not terribly strict, and certainly we know from the simple case of a boost along the x-axis that the components can mix into each other (think about the usual space and time four-vector, and how it transforms).
In general, for a Lorentz transformation, whatever four-vector or tensor you have can have its components mix together pretty generally.
Also, at least in the classical realm, fields NEVER depend on gauge in any way. The issue of gauge fixing only ever comes up when you start working with potentials, which are not measurable. So immediately throw out anything involving gauge dependence when asked about fields.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
|
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
