|
GR8677 #55
|
|
|
Problem
|
|
 |
Statistical Mechanics }Fermi Temperature }Fermi Temperature
When one deals with metals, one thinks of Fermi branding---i.e., stuff like Fermi energy, Fermi velocity, Fermi temperature, etc. So, 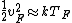 . Fermi stuff is based on the Fermi-Dirac distribution, which assumes that the particles are fermions. Fermions obey the Pauli-exclusion principle. (c.f. Bose-Einstein distribution, where the particles are bosons, who are less discriminating and inclusive than fermions. Both Bose-Einstein and Fermi-Dirac assume indistinguishable particles, but the Boltzmann distribution, which assumes the particles are distinguishable) . Fermi stuff is based on the Fermi-Dirac distribution, which assumes that the particles are fermions. Fermions obey the Pauli-exclusion principle. (c.f. Bose-Einstein distribution, where the particles are bosons, who are less discriminating and inclusive than fermions. Both Bose-Einstein and Fermi-Dirac assume indistinguishable particles, but the Boltzmann distribution, which assumes the particles are distinguishable)
All the other choices are too general, since bosons can also satisfy them. (Moreover, the Born approximation is pretty much the fundamental assumption of all of QM---every single calculation you do involving the interpretation of mod square of wave functions as probability depend on the Born approx!)
|
|
|
Alternate Solutions |
SillyMan
2013-06-19 21:54:37 | The best solution is the following: At zero temperature, fermions must occupy the lowest energy states up to the Fermi energy. These states have finite energy.
(Finite/Zero) >> 1.
In other words, (/kT) >> 1. |  |
|
|
Comments |
fredluis
2019-09-17 02:10:41 | Sounds interesting enough; maybe I\'ll watch out for this kind of solution. carpet cleaners |  | ernest21
2019-08-23 02:03:12 | The divergence of the polarization is related to the total charge density, not the surface charge density. cyclone insider |  | SillyMan
2013-06-19 21:54:37 | The best solution is the following: At zero temperature, fermions must occupy the lowest energy states up to the Fermi energy. These states have finite energy.
(Finite/Zero) >> 1.
In other words, (/kT) >> 1.
SillyMan
2013-06-19 21:55:38 |
(/kT) >> 1*
|
|  | pt6
2012-08-20 10:03:28 | Why degeneracy of states is not appropriate choice? |  | jw111
2008-09-14 12:02:24 | One atom has many discrete energy level. [1 2 3 4 5 ...]
=>Without energy apply, electron occupy the energy level from the lowest[ [x x x 4 5 ...]
When two identical atom come to joint together, we can't have somthing likes
[x x x 4 5 ...]
[x x x 4 5 ...]
because of the Pauli-exclusion principle; electrons can't have the same quantum state in our new molecule. The solution taked by nature is
[x x x 4 5 ...]
[x x x 4.1 5.1 ...]
that is, to our molecule, the energy level becomes
[1 1.1 2 2.1 3 3.1 4 4.1 5 5.1 ......]
When you have 1 mole atoms to form a bulk material, the energy level seems continue-the energy band.
It is Pauli-exclusion principle forcing that electrons can't behave like classical particles when assigning mechanical states. |  | Blake7
2007-07-22 20:50:32 | I actually left this one blank on a practice run because I couldn't quickly resolve that the Born Approximation (for X-sections) isn't applicable here to an electron gas of 'Paulions'
Truth is, I couldn't remember offhand what the Born approximation was, either; now it comes back to me. Moral of the story; under a "No Guesses" strategy, I couldn't gain the point. |  | wzm
2006-11-03 11:24:08 | The electrons form a Fermi Gas. The Pauli exclusion principle keeps electrons from all occupying the ground state in momentum space, and pushes them into higher energy states.
SonOfHam
2010-11-12 00:43:52 |
Yes, this is the most direct answer. In these problems, quick qualitative reasoning is best.
|
flyboy621
2010-11-14 21:33:11 |
yes
|
tatitechno
2011-09-21 07:32:53 |
good (the best answer)
|
Astronaut
2016-02-19 11:06:51 |
Yup
|
|  | einstein
2006-03-29 21:22:13 | Just a clarification of the comment you make at the end->
(Moreover, the Born approximation is pretty much the fundamental assumption of all of QM---every single calculation you do involving the interpretation of mod square of wave functions as probability depend on the Born approx!)
I think you are confusing the "Born Probability interpretation" (ie that the mod square of the wave function= probability density) with the "Born Approximation" (which essentially means to take only the first term in a perturbative series solution to a scattering problem).
nitin
2006-11-16 09:06:51 |
Yes, Yosun's rant about the Born Approximation is definitely wrong. The Born Approximation amounts to taking the first term in the Born expansion. Careful Yosun!
|
SurpriseAttachyon
2015-09-15 21:28:29 |
These forums have made me a lot more confident about my physics abilities... Watching obvious mistakes among the pros is comforting
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
