|
GR8677 #58
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ernest21
2019-08-23 02:03:29 | I solved this by some quick common sense. The group velocity is just the velocity of the particle associated with the wave motion. jenna marbles bikini |  | keradeek
2011-10-12 03:08:15 | I picked E when I tried to solve this problem, because you can recontruct the hologram only with the frequency that you used to construct the hologram. Thus I felt that the hologram 'contains' the information about which frequency is to be used to view it.
However, looking closer at the question, it says what information is 'recorded'. So I guess, technically B is the right answer. |  | padkins
2011-02-06 12:36:10 | just because the light only has a single frequency component doesn't necessarily mean that that frequency isn't recorded by a given experiment. |  | FortranMan
2008-10-27 17:25:59 | how can intensity depend on phase if 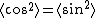 ? ?
a19grey2
2008-11-03 22:37:32 |
Intensity depends on phase in single and double slit diffraction experiments. I suggest reading up on these experiments as an introduction to phase relationships.
|
|  | evanb
2008-06-20 13:21:53 | Just the fact that if you've ever looked at a hologram you can tell that it doesn't retain the color information should rule out III.
neon37
2010-11-03 09:47:49 |
good point!
|
|  | ELC
2007-10-23 18:08:33 | Also, doesn't the "monochromatic light" comment tip you off that it's not III. Isn't "wave-front angular frequency" just the color of the light?
a19grey2
2008-11-03 22:36:32 |
Yes, this is why III is not part of the right answer.
There are holograms (freaking awesome ones) that use polychromatic light and thus record information using I, II, and III. The key here though, is the term monochromatic.
|
alemsalem
2010-09-29 05:43:44 |
isn't "wavefront" angular frequency meaningless, since the wavefront is at the same phase, or does it just mean angular frequency of the whole wave.
|
walczyk
2011-03-09 22:52:05 |
hey alemsalem, um wavefront angular frequency is the frequency of the wave in a reference frame that is moving at the same speed of the wave, so its the frequency the wave changes wrt to time t. more simply, its the rate of change of the phase. so yes, in terms of light it is inversely proportional to the wavelength, which determines the color that we our eyes see. therefore since its a monochromatic light source, (this is a slipper slope argument) a recording of the angular frequency isn't necessary to produce an image since the the incident light's angular frequency has only one state. Hypothetically, a hologram could produce a different image entirely for red incident light than for green incident light. while that is cool, it is not what the question is talking about. phase and amplitude is a big deal. they are related by the heisenberg uncertainty principle. that should tip you off that those two values describe a system like how position and momentum describe a system, and that uncertainty is demanded. anyway, good luck with problems like this on the next test!
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
