|
GR8677 #65
|
|
|
Problem
|
|
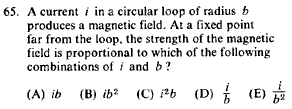 |
Electromagnetism }Biot-Savart Law }Biot-Savart Law
One either remembers the field of a circular current loop or one derives it from the Bigot-Savart Law,
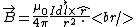
One finds that 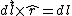 , as they're perpendicular. , as they're perpendicular. 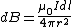 , and the vertical components of the field cancel, thus there are only the horizontal components (parallel to the axis of the ring). , and the vertical components of the field cancel, thus there are only the horizontal components (parallel to the axis of the ring).  is the directest distance from a differential element on the wire to a point on the axis, and is the directest distance from a differential element on the wire to a point on the axis, and  is the horizontal distance (along the axis) from the center of the ring to that point. Thus, the integral becomes, is the horizontal distance (along the axis) from the center of the ring to that point. Thus, the integral becomes,
^{3/2}} = \frac{\mu_0 I b}{2 }\frac{b}{(x^2+b^2)^{3/2}}, <br />
)
where 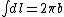 . .
So anyway, the field, at a point anywhere along the axis of the loop is 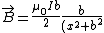^{3/2}}) . .
At a point far, far, away, 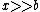 , and thus , and thus 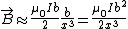 . .
Set  , where , where  is the fixed coordinate of that point, to get that the field is proportional to is the fixed coordinate of that point, to get that the field is proportional to 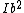 . .
Incidentally, defining the magnetic dipole moment to be 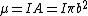 , one finds the field of a magnetic dipole to be , one finds the field of a magnetic dipole to be 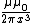 . The field far from a current loop is the same as the field of a magnetic dipole. . The field far from a current loop is the same as the field of a magnetic dipole. |
|
|
Alternate Solutions |
cyberpunk
2010-09-08 15:36:55 | I have a much easier solution utilizing unit analysis. Simple notice that the form of the solution is going to be of the form:rnrn(vaccum permiability)*(current)^a*(radius)^b/(distance)rnrnWhat you need to find is the values of a and b given the final result is in webers. The units are:rnrn[webers/(Amps*meters)]*(Amps)^a*(radius)^b/(meters)rnrngiven this a=1 and b=2. Voila unit analysis will save you. |  | ironman
2008-07-17 11:41:24 | There is an even easier way to solve this problem. Far away from the current loop, the magnetic field can be considered to be that of a dipole. Recall that the dipole moment is defined by 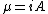 , where , where 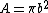 (the area of the current loop). So (the area of the current loop). So 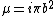 . One can quickly see the correct answer is (B)! . One can quickly see the correct answer is (B)! |  |
|
|
Comments |
physics_guy
2018-08-08 21:23:00 | The field of a magnetic dipole is proportional to the magnetic dipole moment, which is the product of the current and the area of the loop. |  | socolenco_
2015-11-04 15:26:47 | In this problem they\'re asking for the expression of the strength of the magnetic field and using dimensional analysis we find that (D) is the only one with the right units. \r\n\r\n(B) has indeed units of magnetic dipole moment, but I don\'t see how it can be \"proportional\" to the strength of the magnetic field which has different units. The strength of the magnetic field is equal to the magnetic dipole moment over volume, isn\'t it?
GrahamS
2016-10-29 04:34:12 |
Dimensional analysis won\'t work here because they are asking about a proportionality. That implies that there could be constants that they are leaving out, constand that could have totally unknown units. Anyways, I think somebody who took basic E&M shouldn\'t ever forget the formula for the magnetic field outside of a wire of current, which makes this problem extremely quick, even wuicker than those that can be done with dimensional analysis.
|
|  | cyberpunk
2010-09-08 15:36:55 | I have a much easier solution utilizing unit analysis. Simple notice that the form of the solution is going to be of the form:rnrn(vaccum permiability)*(current)^a*(radius)^b/(distance)rnrnWhat you need to find is the values of a and b given the final result is in webers. The units are:rnrn[webers/(Amps*meters)]*(Amps)^a*(radius)^b/(meters)rnrngiven this a=1 and b=2. Voila unit analysis will save you. |  | 511mev
2009-11-05 19:08:35 | This is a logic argument for people who totally forgot everything about E&M: common sense tells us 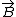 must be proportional to some positive powers of must be proportional to some positive powers of 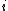 and and 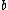 . We know that the length of the loop (and therefore the amount of current . We know that the length of the loop (and therefore the amount of current 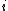 ) increases as radius squared, so the answer must go as ) increases as radius squared, so the answer must go as 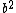 . Only (B) has that. . Only (B) has that.
signminus
2010-08-02 12:35:10 |
Does this actually work? If by the length of the loop you mean its circumference, it actually grows as 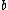 rather than rather than 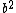 ... ...
|
flyboy621
2010-11-14 22:07:45 |
This solution is not right (dare I say "not even wrong")? The truth is the field is proportional to the magnetic dipole moment, which is proportional to the area enclosed by the current loop.
|
|  | student2008
2008-10-12 06:22:26 | Actually, the solution using magnetic dipole moment is the best one, since there's nothing about the position of the fixed point in the conditions of the problem. It can even lie not on the axis of the loop. |  | ironman
2008-07-17 11:41:24 | There is an even easier way to solve this problem. Far away from the current loop, the magnetic field can be considered to be that of a dipole. Recall that the dipole moment is defined by 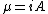 , where , where 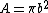 (the area of the current loop). So (the area of the current loop). So 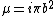 . One can quickly see the correct answer is (B)! . One can quickly see the correct answer is (B)!
monicka1991
2011-10-06 17:22:59 |
great ans!! :)
|
tommy22222
2019-10-13 05:10:40 |
Brilliant answer
|
|  | jax
2005-12-03 07:26:49 | It makes more sense if you say that 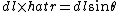 , and if you draw the diagram, , and if you draw the diagram, 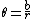 so the Biot-Savart law becomes, so the Biot-Savart law becomes,
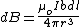 , and , and 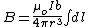 where where 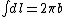
When I first read this solution I was confused as to where the extra b in the numerator comes from. It comes from the sin term in the cross product.
Man this site needs a preview option, I've got my fingers crossed that my latex code is correct and my clarification actually makes sense...
This page might make more sense than the way I typed it...
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/curloo.html#c3
jax
2005-12-03 07:27:54 |
ugh that's actually 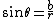 at the beginning. And I forgot how to do a hat on top of a letter in latex, I thought it was at the beginning. And I forgot how to do a hat on top of a letter in latex, I thought it was  but I guess I am wrong? but I guess I am wrong?
|
jax
2005-12-03 07:28:04 |
Oh wait my hat worked that time :)
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
