|
GR8677 #67
|
|
|
|
|
Alternate Solutions |
walczyk
2011-03-04 04:08:25 | Other people have remarked about the errors in the posted solution, which there are a couple big ones, and while there are posts about solving it by approximating by max entropy which is the fastest method, I still thought an instructive "long-way" solution was needed.
I didn't remember the internal energy in terms of partition function at all so I had to look it up. Its 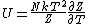 . .
The nifty approximation I didn't remember is 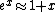 and it really makes this quick work. and it really makes this quick work.
First 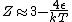 , then churn out , then churn out ) . .
The problem is asking for average energy per particle so that's 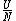 . I think you can figure out the rest,but I'll write out the proper way anyway. . I think you can figure out the rest,but I'll write out the proper way anyway.
The other nifty approximation is 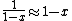 , and if we use it we get , and if we use it we get 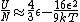 . Cough, drop the second term, and you're done. . Cough, drop the second term, and you're done. |  | kroner
2009-10-08 09:47:38 | If  is the difference in energy between two states, then as is the difference in energy between two states, then as 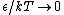 , the ratio of the probabilities of being in each state , the ratio of the probabilities of being in each state 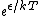 goes to 1, so the states become equally likely (as jakevdp and others point out). goes to 1, so the states become equally likely (as jakevdp and others point out).
Then the average energy of each particle is /3 = 4\epsilon/3) . . |  |
|
|
Comments |
Ronald
2017-10-25 06:21:51 | Notice \"A large 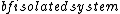 ”! This is microcanonical ensemble.\r\nSo the probability for each state is same! (equal a prior theory)\r\n\r\nThus ”! This is microcanonical ensemble.\r\nSo the probability for each state is same! (equal a prior theory)\r\n\r\nThus /3 = (4/3)\\epsilon) \r\n\r\nChoose (C) \r\n\r\nChoose (C) |  | varsha
2017-01-17 11:10:51 | How did epselon become >> than kT??....please explain, |  | mhendrix61
2014-08-22 13:33:23 | Average is sum over N. 0+1+3/3=4/3 |  | walczyk
2011-03-04 04:08:25 | Other people have remarked about the errors in the posted solution, which there are a couple big ones, and while there are posts about solving it by approximating by max entropy which is the fastest method, I still thought an instructive "long-way" solution was needed.
I didn't remember the internal energy in terms of partition function at all so I had to look it up. Its 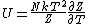 . .
The nifty approximation I didn't remember is 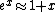 and it really makes this quick work. and it really makes this quick work.
First 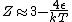 , then churn out , then churn out ) . .
The problem is asking for average energy per particle so that's 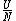 . I think you can figure out the rest,but I'll write out the proper way anyway. . I think you can figure out the rest,but I'll write out the proper way anyway.
The other nifty approximation is 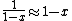 , and if we use it we get , and if we use it we get 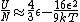 . Cough, drop the second term, and you're done. . Cough, drop the second term, and you're done.
walczyk
2011-03-04 13:09:22 |
a sign error messes things up right at the end: 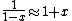 so for a final answer you get so for a final answer you get 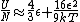
|
jgramm
2014-09-23 22:40:56 |
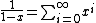 , not , not 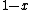 . A counter-example to your approximation is . A counter-example to your approximation is 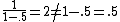
|
|  | kroner
2009-10-08 09:47:38 | If  is the difference in energy between two states, then as is the difference in energy between two states, then as 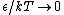 , the ratio of the probabilities of being in each state , the ratio of the probabilities of being in each state 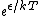 goes to 1, so the states become equally likely (as jakevdp and others point out). goes to 1, so the states become equally likely (as jakevdp and others point out).
Then the average energy of each particle is /3 = 4\epsilon/3) . .
chemicalsoul
2009-11-03 21:23:51 |
This is it ! the average value of a three sided dice. No need for lengthy derivation.
|
Almno10
2010-11-12 00:09:12 |
thats bad ass
|
|  | Jeremy
2007-11-13 12:21:20 | A few things about the long way (official solution)... (1) We don't want the average energy of the system, we want the average energy of each particle. (2) In the first equation for energy 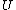 , the , the 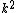 should be replaced by should be replaced by 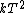 . (3) . (3) 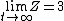 . Also, I think the solution is cleaner using . Also, I think the solution is cleaner using 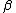 ( (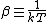 ). ).
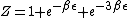
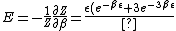}{Z})
As 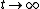 , , 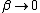 . Therefore the limit causes all exponentials to become . Therefore the limit causes all exponentials to become 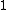 . .
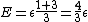 . .
FortranMan
2008-10-28 11:10:05 |
So the absolute temperature is when T 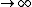 ? Is that what they mean by absolute temperature? ? Is that what they mean by absolute temperature?
|
eliasds
2008-11-03 21:48:34 |
I think by absolute temperature, they are referring to temperature in degrees kelvin.
|
physicsisgod
2008-11-05 21:04:47 |
No, Jeremy is just taking kT >> 1, which makes 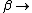 0 0
|
|  | hefeweizen
2006-11-30 12:42:40 | i think there is a typo -
epsilon << kT
beta*epsilon << 1
and you can just use:
sum(E__i*exp(-beta*epsilon))/Z
|  | Andresito
2006-03-18 20:31:05 | jakevdp, thank you for posting your alternate solution. It seems that that is the shortest and the one ETLS wants you to think of.
Yosun, when you have zeta*(Dzeta/Dtemperature) how come that in the remaining exponential terms (second equation) do not have a factor of 2 in their powers?
I think there should be exp(-2 epsilon/kT) and exp(-6 epsilon/kY
eliasds
2008-11-03 21:47:43 |
I think by absolute temperature, they are referring to temperature in degrees kelvin.
|
|  | jakevdp
2005-11-01 11:19:24 | Alternately, you can realize that at kT>>e, Entropy is near maximum, thus each particle has roughly equal probablility of being in any of the three states. Thus, average energy is simply (0+e+3e)/3 = (4/3)e
nitin
2006-11-16 11:17:24 |
Yosun
This long and elaborate calculation is truly inappropriate and silly when it comes to answering a GRE MCQ. As jakevdp pointed out, since 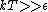 , all 3 possible nondegenerate energy states are equally likely to be occupied by any of the N particles. Therefore, the average energy of each particle would be , all 3 possible nondegenerate energy states are equally likely to be occupied by any of the N particles. Therefore, the average energy of each particle would be 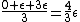 . .
|
grae313
2007-10-07 18:09:55 |
nitin, if you look at all the answers Yosun gives, one could only conclude that he(?) is presenting the rigorous derivation of each solution where applicable, for those who want to see and study the physics behind the solution. I doubt he thinks it is the best solution or the way to approach the ETS exam. This is for studying only.
|
Richard
2007-10-31 18:03:39 |
she...
|
madfish
2007-11-02 16:24:24 |
it. j/p
|
physicsisgod
2008-11-05 21:07:32 |
My long, elaborate, innappropriate and silly calculation shows that nitin is a douche.
|
Herminso
2009-09-01 12:35:18 |
kT>>e means that Entropy is near maximum, and remember that the maximum for the entropy is achieved when the system reach the equilibrium thermodynamic. The Postulate of Equal Priori Probability: When a macroscopic system is in thermodynamic equilibrium, its state is equally likely to be any state satisfying the macroscopic conditions of the system (k. Huang 2ed pag 129).
That justify why each particle has roughly equal probability of being in any of the three states, just as jakevdp did.
|
Setareh
2011-10-26 07:55:39 |
Can anyone tell me why if kT>>e, entropy is near maximum?
|
|  |
|
| Post A Comment! |
You are replying to:
Other people have remarked about the errors in the posted solution, which there are a couple big ones, and while there are posts about solving it by approximating by max entropy which is the fastest method, I still thought an instructive "long-way" solution was needed.
I didn't remember the internal energy in terms of partition function at all so I had to look it up. Its 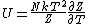 .
The nifty approximation I didn't remember is 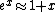 and it really makes this quick work.
First 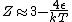 , then churn out ) .
The problem is asking for average energy per particle so that's 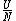 . I think you can figure out the rest,but I'll write out the proper way anyway.
The other nifty approximation is 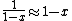 , and if we use it we get 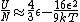 . Cough, drop the second term, and you're done. |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
