|
GR8677 #73
|
|
|
|
|
Alternate Solutions |
secretempire1
2013-04-18 21:09:22 | The purpose of antireflective coating is to make it so that the light is destructively interfered with. You want light entering the coating and leaving the coating to be out of phase by 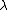 /2. /2.
Therefore, you want the total extra travel distance within the coating to correspond to 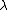 /2. /2.
2*thickness = 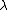 /2 /2
thicnkess = 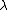 /4 /4 |  | flyboy621
2010-11-15 18:58:54 | Part of the incident wave reflects off the coating and has its phase reversed. The other reflection comes from the boundary between coating and glass, and also has its phase reversed. Thus both reflected waves have their phase changed by the same amount. However, the second one traveled 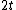 farther. For destructive interference to occur, we must have farther. For destructive interference to occur, we must have
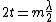
for some odd 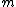 . The only answer that fits this relation is (A). . The only answer that fits this relation is (A). |  |
|
|
Comments |
secretempire1
2013-04-18 21:09:22 | The purpose of antireflective coating is to make it so that the light is destructively interfered with. You want light entering the coating and leaving the coating to be out of phase by 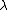 /2. /2.
Therefore, you want the total extra travel distance within the coating to correspond to 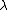 /2. /2.
2*thickness = 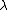 /2 /2
thicnkess = 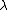 /4 /4
admin
2013-09-10 07:04:57 |
this is incorrect. quantum mechanically, light interferes as particles.
|
|  | flyboy621
2010-11-15 18:58:54 | Part of the incident wave reflects off the coating and has its phase reversed. The other reflection comes from the boundary between coating and glass, and also has its phase reversed. Thus both reflected waves have their phase changed by the same amount. However, the second one traveled 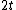 farther. For destructive interference to occur, we must have farther. For destructive interference to occur, we must have
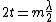
for some odd 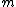 . The only answer that fits this relation is (A). . The only answer that fits this relation is (A).
ali8
2011-06-29 12:49:45 |
Awesome !! thank you :)
|
checkyoself
2011-10-09 08:28:05 |
As I understand it, the formula for destructive interference when there is no relative phase change is 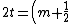\lambda) . For m=0 this still gives lamda/4 for the thickness plus consecutive integer multiples of that. Thought I'd just clarify. . For m=0 this still gives lamda/4 for the thickness plus consecutive integer multiples of that. Thought I'd just clarify.
|
|  | spacemanERAU
2009-10-18 19:45:24 | could someone explain to me why the change in wavelength is 1/2 ? please
neon37
2010-11-03 12:39:26 |
If the phase is shifted by  then you have destructive interference. (think about distance between trough and crest). then you have destructive interference. (think about distance between trough and crest).  phase shift is 1/2 the wavelength. Then to get half wavelength phase shift in the incident and reflected you need half of that distance, which is phase shift is 1/2 the wavelength. Then to get half wavelength phase shift in the incident and reflected you need half of that distance, which is 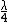
|
Almno10
2010-11-12 17:42:34 |
basically, the reflected waves (one reflected from air/coat boundary, one reflected from the coat/glass boundary) are in phase since both hit a wall with a greater index of refraction. So the path length difference must account for a half wavelength. This path length difference is 2t.
|
|  | claire
2009-10-07 13:35:29 | Yosun, thank you so much for this awesome site. It has been incredibly helpful for my exam this saturday. I dont know what I would have done with out it.
When the second beam passes through the first interface its not shifted, the shift just comes from the reflection. so the two waves are both shifted by 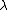 /2 due to reflection, and the second wave travels an extra 2t, which is the only source of the difference, so /2 due to reflection, and the second wave travels an extra 2t, which is the only source of the difference, so
2t=(m+1/2)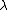 as you have. as you have.
Mr.Moist
2018-10-20 20:38:17 |
Amen to that
|
|  | vsravani
2008-11-02 18:44:34 | If anybody wants to get a clear explanation on thin film interference, they can go through
http://physics.bu.edu/~duffy/PY106/Diffraction.html
It really gives a very good explanation with a step by step procedure and figures. |  | wangjj0120
2008-08-27 08:29:21 | No~
the change in wavelength is not 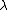 /2. /2.
When the incident wave (I) touches the coating, the first reflecting wave (R1) occurs and its phase was changed by pi, while the transmitting waves enter coating (T1) without changing phase. The second reflecting wave (R2) occurs when T1 touches glass, and phase of R2 was changed by pi (assum n(glass) > n(coating) > n(air) ). R2 touches interface between coating and air and then transmits into air, that is T2. T2 is in phase with R2. (phase of transmission at interface does't change). So the phase of R2 changes by pi due to interface happens only ONCE.
|  | madfish
2007-11-02 16:41:41 | this question is ambiguous. It really needs to state that the coating is on BOTH sides on the glass, otherwise the math does not work out (since there wouldn't be a 180 degree phase shift on the back wall). However the problem states "it is necessary to coat a glass with A non-reflecting layer (A = one)" those ETS assholes.
jesford
2008-04-01 21:39:16 |
The coating is only on one side of the glass. There is a 180 degree phase shift upon reflection at BOTH the air-coating interface and the coating-glass interface, because in both cases the index of refraction is greater in the material that the light is reflecting off of, than it is in the material in which the light propagates. In other words, n(coating)>n(air), and n(glass)>n(coating).
|
livieratos
2011-11-08 05:24:15 |
isn't this the other way around? i thought when the index where the incident light is, is greater than the index of the medium at the reflection point, the phase shift is zero...rncorrect me if i'm wrong please
|
livieratos
2011-11-08 05:25:12 |
though the result is still the same...
|
|  | Mindaugas
2007-09-28 08:16:07 | Some explanation http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
nontradish
2012-04-17 10:47:39 |
I think the URL should be: http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/antiref.html
|
|  | irishroogie
2007-09-04 23:07:11 | I still don't get the line, "The change in wavelength occurs over twice the thickness t of the coating, thus " Why 2x the thickness?
jive
2007-10-02 22:39:02 |
I believe it's because the light passes through the thickness twice -- once going in, and once coming out after being reflected.
|
|  | nitin
2006-11-16 12:35:58 | "Destructive interference is thus given by a half-integer wavelength change 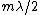 , where the smallest change is , where the smallest change is 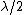 ." ."
Hmm.. well, the uninformed or careless would be inclined to think that your 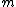 would assume any positive integral value, which will not be true for destructive interference. I guess you should have pointed out that would assume any positive integral value, which will not be true for destructive interference. I guess you should have pointed out that 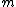 should be an odd number, or simply use the form should be an odd number, or simply use the form \lambda) , , 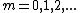 instead. instead.
This question seems to presume a minimum thickness for the coating (I guess that is what is meant by "best choice"), which would then justify taking 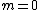 , or in your case , or in your case 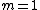 . . |  |
|
| Post A Comment! |
You are replying to:
"Destructive interference is thus given by a half-integer wavelength change 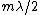 , where the smallest change is 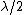 ."
Hmm.. well, the uninformed or careless would be inclined to think that your 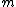 would assume any positive integral value, which will not be true for destructive interference. I guess you should have pointed out that 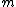 should be an odd number, or simply use the form \lambda) , 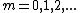 instead.
This question seems to presume a minimum thickness for the coating (I guess that is what is meant by "best choice"), which would then justify taking 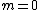 , or in your case 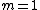 . |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
