|
GR8677 #81
|
|
|
|
|
Alternate Solutions |
camarasi
2017-10-25 15:31:51 | The easiest way is if you remember the equation: 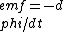 which has units which has units ![[Bfield] \\times [Area] / [Time]](/cgi-bin/mimetex.cgi?[Bfield] \\times [Area] / [Time]) . \r\n\r\nSince this involves a time derivative, eliminate A and D: the given . \r\n\r\nSince this involves a time derivative, eliminate A and D: the given  term has to be a term has to be a  . \r\n\r\nRecognize that the form (excluding numerical factors) . \r\n\r\nRecognize that the form (excluding numerical factors) 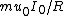 has units of B-field - think of the field of a current loop. Mentally extract a (b) term from the denominators of answers B, C, and E into the parenthesis and consider it a B-field. Now you need to look for the has units of B-field - think of the field of a current loop. Mentally extract a (b) term from the denominators of answers B, C, and E into the parenthesis and consider it a B-field. Now you need to look for the ![[Area]\\[time]](/cgi-bin/mimetex.cgi?[Area]\\[time]) term.\r\n\r\nEliminate E now: no time dependence.\r\n\r\nEliminate C: No term.\r\n\r\nEliminate E now: no time dependence.\r\n\r\nEliminate C: No ![[Area]](/cgi-bin/mimetex.cgi?[Area]) term.\r\n\r\nB is the correct answer: both area term term.\r\n\r\nB is the correct answer: both area term 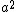 and time term and time term 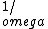 exist. \r\n\r\n\r\n\r\n\r\n exist. \r\n\r\n\r\n\r\n\r\n |  | ramparts
2009-11-06 10:55:30 | Here's yet another quick GRE-type approach (if you're good with units) - remembering or deriving that a weber is a volt-second, and using the definition of 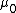 from the front of the test, you can rule out all but A and B based on units. Now, if from the front of the test, you can rule out all but A and B based on units. Now, if 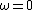 then there's a non-zero but constant current in the outer loop. This isn't going to induce anything, so pick the one with the sine term, as that goes to 0 in that limit. then there's a non-zero but constant current in the outer loop. This isn't going to induce anything, so pick the one with the sine term, as that goes to 0 in that limit. |  | wittensdog
2009-07-27 12:13:32 | The way I approached it was to remember the two things which seem to be what ETS is looking for here. One is that there is a time derivative, which should create a term of the form w * sin (wt). That eliminates A, D, and E, the first two because they have cosine instead of sine, and the last one because there is no w that comes out front out of the cos(wt) as a result of the chain rule. The second is that since the inner loop is said to be very small compared to the larger loop, you can take the field to be roughly the same over the inner loop, and so the flux should be proportional to the area of the inner loop, which goes with a^2. All of the parenthetical terms are the same, so this leaves only B. Then I guess for free you get the fact that there should be a single factor of b in the bottom. That analysis seems faster to me than unit checking. |  | dicerandom
2006-09-06 20:46:32 | There's another way to think through this which doesn't involve having to remember (or derive) the magnetic field of the loop.
We know that the field generated by the loop will have a cos(wt) dependence since the current has that dependence. Thus the EMF must have a sin(wt) dependence and we can eliminate the options involving cos(wt). Of the remaining options only (B) has the proper units (mu0 ~ gauss/(meter*ampere) ). |  |
|
|
Comments |
casseverhart13
2019-08-15 08:50:40 | Good Problem Examine and fascinating. refrigerator repair |  | camarasi
2017-10-25 15:31:51 | The easiest way is if you remember the equation: 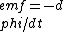 which has units which has units ![[Bfield] \\times [Area] / [Time]](/cgi-bin/mimetex.cgi?[Bfield] \\times [Area] / [Time]) . \r\n\r\nSince this involves a time derivative, eliminate A and D: the given . \r\n\r\nSince this involves a time derivative, eliminate A and D: the given 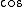 term has to be a term has to be a 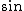 . \r\n\r\nRecognize that the form (excluding numerical factors) . \r\n\r\nRecognize that the form (excluding numerical factors) 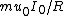 has units of B-field - think of the field of a current loop. Mentally extract a (b) term from the denominators of answers B, C, and E into the parenthesis and consider it a B-field. Now you need to look for the has units of B-field - think of the field of a current loop. Mentally extract a (b) term from the denominators of answers B, C, and E into the parenthesis and consider it a B-field. Now you need to look for the ![[Area]\\[time]](/cgi-bin/mimetex.cgi?[Area]\\[time]) term.\r\n\r\nEliminate E now: no time dependence.\r\n\r\nEliminate C: No term.\r\n\r\nEliminate E now: no time dependence.\r\n\r\nEliminate C: No ![[Area]](/cgi-bin/mimetex.cgi?[Area]) term.\r\n\r\nB is the correct answer: both area term term.\r\n\r\nB is the correct answer: both area term 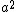 and time term and time term 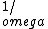 exist. \r\n\r\n\r\n\r\n\r\n exist. \r\n\r\n\r\n\r\n\r\n |  | ramparts
2009-11-06 10:55:30 | Here's yet another quick GRE-type approach (if you're good with units) - remembering or deriving that a weber is a volt-second, and using the definition of 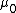 from the front of the test, you can rule out all but A and B based on units. Now, if from the front of the test, you can rule out all but A and B based on units. Now, if 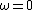 then there's a non-zero but constant current in the outer loop. This isn't going to induce anything, so pick the one with the sine term, as that goes to 0 in that limit. then there's a non-zero but constant current in the outer loop. This isn't going to induce anything, so pick the one with the sine term, as that goes to 0 in that limit.
natestree
2011-09-22 11:39:38 |
But B is the answer...
|
michael
2011-10-08 15:04:37 |
This doesn't work. If 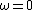 both (a) and (b) go to zero. both (a) and (b) go to zero.
|
|  | wittensdog
2009-07-27 12:13:32 | The way I approached it was to remember the two things which seem to be what ETS is looking for here. One is that there is a time derivative, which should create a term of the form w * sin (wt). That eliminates A, D, and E, the first two because they have cosine instead of sine, and the last one because there is no w that comes out front out of the cos(wt) as a result of the chain rule. The second is that since the inner loop is said to be very small compared to the larger loop, you can take the field to be roughly the same over the inner loop, and so the flux should be proportional to the area of the inner loop, which goes with a^2. All of the parenthetical terms are the same, so this leaves only B. Then I guess for free you get the fact that there should be a single factor of b in the bottom. That analysis seems faster to me than unit checking.
flyboy621
2010-11-15 19:23:19 |
Yes
|
lelandr
2011-04-24 22:41:47 |
+1 for this solution
|
|  | wangjj0120
2008-08-28 07:55:38 | I think 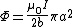 is incorrect because is incorrect because 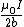 is the magnetic field only at the center. Magnetic field induced by the outer current should be a function of r, that is B=B(r). To get the magnetic flux, we should integrate is the magnetic field only at the center. Magnetic field induced by the outer current should be a function of r, that is B=B(r). To get the magnetic flux, we should integrate 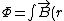\cdot d\vec{A}) instead of instead of 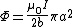 . .
gt2009
2009-06-25 16:38:29 |
It said approximately equal to.
|
|  | ivalmian
2008-04-03 21:54:38 | Just a little notice - you can't use Ampere Law for this problem, instead use Biot-Savart.
syreen
2013-09-12 19:15:46 |
Why not? I can't figure out why, but Amperes gives me an e0 instead of pi and switches b and a.
|
|  | dicerandom
2006-09-06 20:46:32 | There's another way to think through this which doesn't involve having to remember (or derive) the magnetic field of the loop.
We know that the field generated by the loop will have a cos(wt) dependence since the current has that dependence. Thus the EMF must have a sin(wt) dependence and we can eliminate the options involving cos(wt). Of the remaining options only (B) has the proper units (mu0 ~ gauss/(meter*ampere) ). |  | imrebartos
2005-11-09 07:11:15 | |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
