|
GR8677 #83
|
|
|
Problem
|
|
 |
Atomic }Spectral Line }Spectral Line
The less dense a gas is, the more precise (thin) its emission lines. So, when one has a dense gas, one expects the spectral lines to be broader---as in choice (C).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
msdec
2016-09-16 21:24:56 | Another way to think about it:\r\n\r\nAssume the gas is ideal (PV = nRT), if the density increases with constant V, P increases and so does T. With higher T means higher rms speeds of the atoms which could be traveling radially toward you and away, leading to a doppler shift toward both red and blue, or a \"broadening\" of the spectral lines. |  | shak
2010-08-01 08:52:45 | Impact pressure broadening: The collision of other particles with the emitting particle interrupts the emission process. The duration of the collision is much shorter than the lifetime of the emission process. This effect depends on both the density and the temperature of the gas. The broadening effect is described by a Lorentzian profile and there may be an associated shift.
Quasistatic pressure broadening: The presence of other particles shifts the energy levels in the emitting particle, thereby altering the frequency of the emitted radiation. The duration of the influence is much longer than the lifetime of the emission process. This effect depends on the density of the gas, but is rather insensitive to temperature. The form of the line profile is determined by the functional form of the perturbing force with respect to distance from the perturbing particle. There may also be a shift in the line center.
pam d
2011-09-26 21:48:40 |
Duh.
|
|  | student2008
2008-10-14 02:44:05 | Maybe ETS also implied that in a dense gas  broadening is higher (due to more intensive movement of atoms). broadening is higher (due to more intensive movement of atoms). |  | dannyboytward
2008-10-11 20:09:56 | It sounds like what the question is getting at, saying that the time between collisions is much less than the lifetime of the state, is a time-energy uncertainty relation. States that exist for a short amount of time have more uncertainty in their energy, and thus broader spectral lines.
smokwzbroiplytowej
2008-10-26 19:40:22 |
Yeah... It seems that Yosun (may he live forever!) just paraphrased answer (C). I agree with dannyboytward:
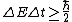
Higher density  shorter lifetime of the states shorter lifetime of the states  higher uncertainty in energy higher uncertainty in energy 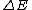 , which is the width of the spectral line. , which is the width of the spectral line.
A good follow up problem is in Serway's 'Modern Physics' (3. ed):
Problem 5.25 (p.189)
"An excited nucleus with lifetime of 0.100 ns emits a  ray of energy 2.00 MeV. Can the energy width (uncertainty in energy, ray of energy 2.00 MeV. Can the energy width (uncertainty in energy, 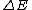 ) of this 2.00 MeV ) of this 2.00 MeV  emission line be directly measured if the best gamma detectors can measure energies to emission line be directly measured if the best gamma detectors can measure energies to 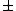 5 eV?" 5 eV?"
|
ali8
2011-06-30 22:28:55 |
@smokwzbroiplytowej: that problem (5.25) is
interesting, could you give us the solution? I think
the answer of the problem is Yes.
|
|  | chrisfizzix
2008-10-03 13:57:43 | Sorry Yosun, but I find your solution here rather lacking.
To think about this from some simple physical principles: each time an atom in the gas collides with another atom, any number of possible exchanges of energy could occur. If we imagine the gas as initially populated exclusively with atoms in the state responsible for the emission line, then most of these atoms will interact with another atom before they get a chance to decay. This means that the possible range of energies of emission from an observer outside the gas is wider - many atoms will still decay to produce the original line, but many others will have absorbed or given up some energy to/from another atom, and decay later with different energies.
Thus, the line will appear broadened by this interaction process. Choice C.
We can also eliminate some of the others for fun:
B: there is nothing in this problem to indicate anything about the polarization of the line. Toss this choice.
D: This would imply that the process going on in the gas is something besides random.
E: More atoms don't cause splitting - an applied magnetic field might, but there's still no information in the problem to net an answer this specific.
Almno10
2010-11-12 18:28:57 |
Don't crap in the gift horse's mouth, though.
|
BillNyeTheRussianSpy
2018-05-22 02:28:36 |
Don\'t look a crap mouth in the horse, as they say.
|
|  | bat_pesso
2007-10-29 12:19:19 | broad emission lines=many energy levels=hotter gas.
colder gas=fewer energy levels=narrower line
Almno10
2010-11-12 18:31:11 |
How about denser gas => more particles => probability of observing outliers increase => fatter line.
|
neo55378008
2012-09-06 12:41:53 |
My thought process was similar. Broader lines means more uncertainty, 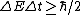
There is no indication the measurments were taking over a longer period of time, so the uncertainty must be do to an increase in energy.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
