|
GR8677 #93
|
|
|
Problem
|
|
 |
Mechanics }Power }Power
Recall the following basic formulas, 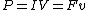 , where , where 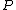 is power, is power, 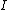 is current, is current, 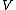 is voltage, is voltage, 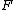 is force, and is force, and  is velocity. is velocity. 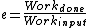 , where , where  is the efficiency, which relates work (and thus power). is the efficiency, which relates work (and thus power).
The problem gives 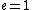 , , 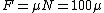 , , 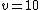 , ,  , ,  ---where all units are SI. ---where all units are SI.
Thus 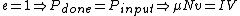 . Solve for . Solve for 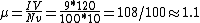 , as in choice (D). , as in choice (D).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
-trous.
2013-10-04 04:44:15 | F * x=P*t)=>F=P/v=9*120/10=108.
F=u*N)=>u=108/100=1.08 |  | newtonsfourth
2009-07-20 16:16:16 | Aluminum in contact with another piece of aluminum has a coefficient of friction greater than 1 so it shears instead of slides. interesting thing to see |  | Poop Loops
2008-09-23 21:04:09 | Not only did I think that you couldn't have a CoF > 1, since friction is only a retarding force, but I also thought "normal" meant "normal to the surface". I had no idea it was pushing parallel to the surface. I just didn't understand how a vertical force related to the parallel energy being released.
Apparently you CAN have CoF > 1, though.
CaspianXI
2009-03-14 15:10:28 |
No, the normal force IS normal to the surface. It's the force of friction that's pushing parallel to the surface.
The force of friction (parallel to the surface) is directly related to the normal force (normal to the surface). An intuitive way to think about this is if you lift the sander off of the surface (normal force = 0), the frictional force goes away. If you push down really hard (normal force increases), the frictional force increases.
|
|  | Furious
2007-11-01 18:40:00 | Was I the only one who thought that you couldn't have a coefficient of friction greater than one?
shak
2010-08-01 09:23:55 |
you are not the only one, i also thought so:))
|
his dudeness
2010-08-19 18:37:17 |
Yeah I definitely fell for it too... Here's Wikipedia to the rescue: "Occasionally it is maintained that µ is always < 1, but this is not true. While in most relevant applications µ < 1, a value above 1 merely implies that the force required to slide an object along the surface is greater than the normal force of the surface on the object. "
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
