\prob{14}
The total energy of a blackbody radiation source is collected for one minute and used to heat water. The temperature of the water increases from 20.0 degrees Celsius to 20.5 degrees Celsius. If the absolute temperature of the blackbody were doubled and the experiment repeated, which of the following statements would be most nearly correct?
- The temperature of the water would increase from 20 degrees Celsius to a final temperature of 21 degrees Celsius.
- The temperature of the water would increase from 20 degrees Celsius to a final temperature of 24 degrees Celsius.
- The temperature of the water would increase from 20 degrees Celsius to a final temperature of 28 degrees Celsius.
- The temperature of the water would increase from 20 degrees Celsius to a final temperature of 36 degrees Celsius.
- The water would boil within the one-minute time period
|
Statistical Mechanics }Blackbody Radiation Formula }Blackbody Radiation Formula
Recall
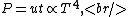
where 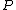 is the power and is the power and  the energy and the energy and 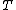 the temperature. the temperature.
So, initially, the blackbody radiation emits 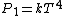 . When its temperature is doubled, it emits . When its temperature is doubled, it emits 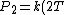^4=16kT^4) . .
Recall that water heats according to 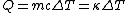 . So, initially, the heat gain in the water is . So, initially, the heat gain in the water is 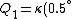) . Finally, . Finally, 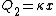 , where , where  is the unknown change in temperature. is the unknown change in temperature.
Conservation of energy in each step requires that 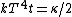 and and 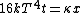 , i.e., that , i.e., that 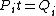 . Divide the two to get . Divide the two to get 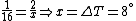 . Assuming the experiment is repeated from the same initial temperature, this would bring the initial . Assuming the experiment is repeated from the same initial temperature, this would bring the initial 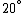 to to 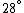 , as in choice (C). , as in choice (C).
|
