GREPhysics.NET: GR9277 #55

GR9277 #55

Problem

GREPhysics.NET Official Solution

\prob{55}

A rectangular loop of wire with dimensions shown above is coplanar with a long wire carrying current I. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated.

What is the magnitude of the net force on the loop when the induced current is i?

$\frac{\mu_0 i I}{2\pi} ln(\frac{r+a}{r})$
$\frac{\mu_0 i I}{2\pi} ln(\frac{r}{r+a})$
$\frac{\mu_0 i I}{2\pi} ln(b/a)$
$\frac{\mu_0 i I}{2\pi} ln(\frac{ab}{r(r+a)})$
$\frac{\mu_0 i I}{2\pi} ln(\frac{r(r+a)}{ab})$

Electromagnetism $\Rightarrow$ }Magnetic Force

The magnetic force of a wire is given by $\vec{F} = I \vec{l} \times \vec{B}$ , where I is the current of the wire and l its length.

The field that produces the force on the loop is given by the long wire (see the previous problem for why). The field of that wire is given trivially by Ampere's Law to be $\vec{B}=\frac{\mu_0 I}{2\pi r}$ , where r is the radial distance away from its center.

Only two wires from the loop contribute to the force, since the cross-product yields 0 force for the two horizontal components. Thus, the net force on the loop with current i with vertical components of length b is $|F_{left}+F_{right}|=|ib\frac{\mu_0 I}{2\pi}\left(\frac{1}{r} - \frac{1}{r+a}\right)|$ . Combine the fraction to get choice (D).

Alternate Solutions

jmason86
2009-09-06 16:13:03

lots of solutions up here already but...

There's no reason that ln should come into this calculation. Eliminate (A) and (B)
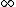As other have said, as r--> $\infty$ F-->0. Eliminates (C) and (E)

Reply to this comment

Comments

jmason86
2009-09-06 16:13:03

lots of solutions up here already but...

There's no reason that ln should come into this calculation. Eliminate (A) and (B)
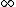As other have said, as r--> $\infty$ F-->0. Eliminates (C) and (E)

Reply to this comment

neutrinosrule
2008-10-04 17:36:00

you can just note that the force has to be inversely proportional to the distance from the loop to the wire... this only leaves D.

Reply to this comment

spacebabe47
2007-08-28 14:55:13

there is no ln in answers C,D,and E

Reply to this comment

bootstrap
2007-04-06 12:51:52

An easy way to do this without paying too much attention to the different forces is looking at the solutions as the limit of r goes to infinity. The only answer that clearly goes to zero is choice D.

hassanctech
2007-09-30 21:16:47

That isn't true. In choices a and b the ln(r/(r+a)) and ln ((r+a)/r) both go to ln(1) as r --> infinity and ln(1) = o so choices 1 and 2 also go to zero.

Reply to this comment

spacebabe47
2006-11-01 15:13:59

If the area of the loop is zero, there will be no flux, and hence no induced current and no force. So, F=0 if a=0. This eliminates A, B, and C. Also, F=0 if b=0. This eliminates E. Only choice D is left.

spacebabe47
2006-11-01 15:23:30

Edit:

If the area of the loop is zero, there will be no flux, and hence no induced current and no force. So, F=0 if a=0. This eliminates C. Also, F=0 if b=0. This eliminates A, B, and E. Only choice D is left.

Reply to this comment

senatez
2006-10-31 20:47:42

You can also consider the limiting case where the force will go to zero as r goes to zero. This will eliminate choices C and E. From here you can make an educated guess. One would expect the force to depend on both dimensions a and b. So then chose choice D.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone