|
GR9277 #57
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Rosenlicht
2011-11-08 14:00:08 | I think you mean that the flux is constantly increasing or decreasing, but the change in flux is constant and of course discontinuous when you go from increasing flux to decreasing flux. |  | mike
2010-10-06 17:38:38 | As noted by herrphysik, 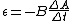 . So the emf is only dependent on the fact that the area is changing, and not dependent on how much area is currently enclosed (this is specific to this problem). Answer B is a trick, since you see the area increasing and decreasing. Once the entire semicircle is in the B field, . So the emf is only dependent on the fact that the area is changing, and not dependent on how much area is currently enclosed (this is specific to this problem). Answer B is a trick, since you see the area increasing and decreasing. Once the entire semicircle is in the B field, 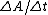 goes from positive to negative, but | goes from positive to negative, but |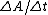 | remains fixed. Thus, answer A is the correct one. | remains fixed. Thus, answer A is the correct one. |  | Maxwells_Demon
2008-09-21 08:48:59 | Given the negative sign in Faraday's Law, wouldn't the induced emf in choice (A) be negative at t=0 rather than positive?
Kabuto Yakushi
2010-09-18 09:21:56 |
I know this is a two year old post but i just thought of a solution, so I'm posting for everyone. Remember that B is a vector and written as 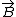 . Take the diagram to be on the x-y plane, one will see that . Take the diagram to be on the x-y plane, one will see that 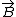 is in the negative direction hence is in the negative direction hence 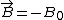 . So the minus signs cancel out. . So the minus signs cancel out.
|
|  | boundforthefloor
2006-11-20 23:09:45 | herrphysik is right, I'd like to add the formula clarification 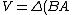/\Delta(t)=\Delta\Phi/\Delta t)
agaliarept
2006-12-01 18:11:03 |
Thank you. Just what I needed.
|
|  | Andresito
2006-03-28 07:01:54 | I thought that choice (B) was the correct one.
The change in the flux "with" respect to time at t=0s is zero. The only graph that show this is (B).
Intead of saying, "The change in flux is constantly increasing as the loop spins into the field, and it is constantly decreasing as it spins out of the field" it would be better to say that "the flux change is discontinous".
herrphysik
2006-08-24 20:47:18 |
The result would be something like (B) if Faraday's Law said that the emf were proportional to the total magnetic flux through the circuit, but it doesn't. It says that the emf is proportional to the RATE OF CHANGE OF MAGNETIC FLUX, and the circuit here being a semi-circle spinning with constant angular velocity, the rate of chage of magnetic flux is CONSTANT.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
