|
GR9277 #58
|
|
|
|
|
Alternate Solutions |
ETScustomer
2017-09-23 18:07:55 | For those who would rather not use the method of elimination:\r\n\r\nFirst use up two (two because spin up and spin down are different states) electrons to fill the =(1,0)) . These two electrons give us the . These two electrons give us the 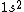 . Then, use up another two electrons to get the . Then, use up another two electrons to get the 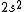 for for =(2,0)) . Then, use up six more electrons to fill the . Then, use up six more electrons to fill the =(2,1)) , and that gives the , and that gives the 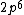 . We\'ve used up now ten electrons, so place the final electron in the . We\'ve used up now ten electrons, so place the final electron in the =(3,0)) shell to get a shell to get a 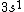 . Altogether, this state is notated as . Altogether, this state is notated as 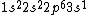 .\r\n\r\nFor higher atomic number atoms, the way of filling the shells to get the ground state is a little more elaborate than the pattern that I used here might suggest. See https://en.wikipedia.org/wiki/Aufbau_principle#Madelung_energy_ordering_rule for more about this. .\r\n\r\nFor higher atomic number atoms, the way of filling the shells to get the ground state is a little more elaborate than the pattern that I used here might suggest. See https://en.wikipedia.org/wiki/Aufbau_principle#Madelung_energy_ordering_rule for more about this. |  |
|
|
Comments |
deneb
2018-10-13 23:23:14 | If you know enough about orbitals to eliminate 4 answers, it would be way quicker to just figure out the correct configuration for 11 electrons and pick C |  | ETScustomer
2017-09-23 18:07:55 | For those who would rather not use the method of elimination:\r\n\r\nFirst use up two (two because spin up and spin down are different states) electrons to fill the =(1,0)) . These two electrons give us the . These two electrons give us the 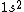 . Then, use up another two electrons to get the . Then, use up another two electrons to get the 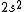 for for =(2,0)) . Then, use up six more electrons to fill the . Then, use up six more electrons to fill the =(2,1)) , and that gives the , and that gives the 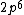 . We\'ve used up now ten electrons, so place the final electron in the . We\'ve used up now ten electrons, so place the final electron in the =(3,0)) shell to get a shell to get a 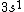 . Altogether, this state is notated as . Altogether, this state is notated as 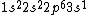 .\r\n\r\nFor higher atomic number atoms, the way of filling the shells to get the ground state is a little more elaborate than the pattern that I used here might suggest. See https://en.wikipedia.org/wiki/Aufbau_principle#Madelung_energy_ordering_rule for more about this. .\r\n\r\nFor higher atomic number atoms, the way of filling the shells to get the ground state is a little more elaborate than the pattern that I used here might suggest. See https://en.wikipedia.org/wiki/Aufbau_principle#Madelung_energy_ordering_rule for more about this. |  | diggydax
2015-03-23 12:27:14 | I'm a little confused about notation in chemistry. In Quantum Mechanics, the notation of (2s+1)^L_(j) is used where L is a place holder for the total angular momentum quantum number (l=0 ->S, l=1->P, l=2 ->D, etc). How does 2s+1 relate to the proton number, in this case Z=11. The solution says to sum up the superscripts to see which add up to 11 but why? |  | blackerester
2012-04-16 22:24:54 | This is learned in chemistry isn't it? I'm an astrophysics major and chemistry is not a requirement so all the atomic orbital and spectroscopic notation questions are foreign to me.
mpdude8
2012-04-20 00:00:06 |
It's definitely taught in basic chemistry, but it's also very relevant to Quantum Mechanics and Electromagnetism. I remember discussing this topic in my first E&M class when going over paramagnetism/ferromagnetism.
In fact, this atomic and spectroscopic stuff actually originates from Quantum Mechanics (spin, angular momentum, etc.)... introductory college chemistry courses just simplify it tremendously.
|
|  | hoyas08
2008-06-17 15:48:49 | Choice (B) should read: 1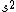 2 2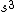 2 2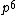 | 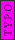 | neutrino
2007-11-02 10:27:37 | should we read;
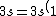)
?
Because else choice C does not add to 11 electrons (2+2+6=10)
neutrino
2007-11-02 10:29:06 |
oeps, latex does not catch my brackets:
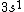
it should be...
|
evanb
2008-06-23 19:40:06 |
Yes, 3s should be read as 3s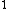 . Otherwise, you wouldn't write it at all, or you would specify 3s . Otherwise, you wouldn't write it at all, or you would specify 3s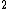 . .
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
