|
GR9277 #59
|
|
|
|
|
Alternate Solutions |
cakedamber
2005-11-11 22:22:50 | Sorry about the null post above, I was getting the hang of your interface. Anyhow, I'm sorry to say this, but your explanation above is flat-out wrong. The singlet state is when the total SPIN angular momentum is 0, i.e. when 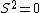 . You're absolutely right that in the . You're absolutely right that in the 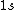 state, state, 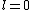 , but , but 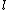 is ORBITAL angular momentum, not spin angular momentum, so that's irrelevant. The reason the ground state of helium must be a singlet is more complicated. Electrons are fermions, which means that the overall wavefunction for two electrons must be antisymmetric. In the ground state of helium, both electrons are in the same spatial state, meaning that their combined spatial wavefunction is symmetric. Therefore, in order to keep their overall combined wavefunction antisymmetric, their combined spin wavefunction must be antisymmetric -- meaning that they are in a spin singlet state, and thus (A) is the right answer. is ORBITAL angular momentum, not spin angular momentum, so that's irrelevant. The reason the ground state of helium must be a singlet is more complicated. Electrons are fermions, which means that the overall wavefunction for two electrons must be antisymmetric. In the ground state of helium, both electrons are in the same spatial state, meaning that their combined spatial wavefunction is symmetric. Therefore, in order to keep their overall combined wavefunction antisymmetric, their combined spin wavefunction must be antisymmetric -- meaning that they are in a spin singlet state, and thus (A) is the right answer. |  |
|
|
Comments |
Maxwells_Demon
2008-09-28 04:17:20 | How do you deal with the spin from the 2 protons from the He in your justifications? I'm a bit confused still...
Poop Loops
2008-10-25 15:52:20 |
I think it's because there are also only 2 protons and they are in the ground state, so they have to have 0 total spin. If they had the same spin, they would have to be in different states, so that's no longer the ground state.
I am just confused about Helium-3 because you end up with 1 neutron instead of 2, so I don't know what that does to the particle's angular momentum, but I guess that won't be on the test since it's more complicated.
|
PhyAnnie
2008-11-06 05:34:56 |
Actually I don't think there' s anything to do with the proton or neutron. We only need to focus on the two electrons and think of their states. (The wave function we've all been discussing is about electrons.)
|
neon37
2010-11-12 01:10:09 |
I think Annie is correct. This question has nothing to do with the particle's total spin. But rather just the electron's spins in the orbitals.
|
raymondtco
2010-11-12 20:17:57 |
But it does not say we are focusing on the helium though. It says "the ground sate of the helium atom", which implies we need to look at the entire "helium" system.
|
troy
2018-03-14 16:10:08 |
He nuclei has 2 protons, 2 neutrons. For the protons (Z), if we consider the shell model, the 2 protons will occupy the ) state, the multiplicity of which is 2. Hence the proton shell is fully filled. Same thing can be said for the neutrons: the 2 neutrons fill completely their state, the multiplicity of which is 2. Hence the proton shell is fully filled. Same thing can be said for the neutrons: the 2 neutrons fill completely their ) state as well. Then just remember that the spin of fully filled (nuclear) shells is always 0. Hence the He nuclei will contribute 0 spin total to the He atom. \r\n\r\nSo it turns out that the He nuclei spin is irrelevant either way: Only the spins from the electrons matter (but as we know, the spins of the 2 electrons cancel each other out as well in the electronic state as well. Then just remember that the spin of fully filled (nuclear) shells is always 0. Hence the He nuclei will contribute 0 spin total to the He atom. \r\n\r\nSo it turns out that the He nuclei spin is irrelevant either way: Only the spins from the electrons matter (but as we know, the spins of the 2 electrons cancel each other out as well in the electronic 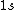 state. So overall spin is 0, and it will thus be in a singlet state. state. So overall spin is 0, and it will thus be in a singlet state.
|
|  | ewhite2
2007-10-27 12:41:27 | The solution still isn't entirely correct. The spin triplet state also has a s = 0 possibility, so this narrows it down to the singlet and triplet state. You still need to take into account the symmetry of the spatial and spin wave functions as in cakedamber's solution.
kaic
2013-10-11 14:59:14 |
Singlet: S = 0
Doublet: S = 1/2
Triplet: S = 1
|
kaic
2013-10-11 15:05:12 |
Further, the total spin state 2S+1 defines the singlet, doublet, etc.
Singlet: 2S+1 = 1, S =0
Doublet: 2S+1 = 2, S = 1/2
Triplet: 2S+1 = 3, S = 1
|
calcuttj
2014-09-03 16:09:10 |
To clarify what kaic is saying.
When adding 2 states of intrinsic spin 1/2, a triplet and a singlet state arise. There is NO doublet state for these particles.
In the singlet state, one particle is up and the other down. The spin-ket is |00> =(1/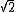 )(| )(|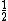 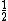 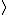 | |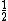 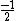 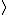 - | - |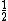 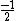  | |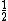 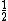 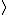 ) )
In the triplet state, the particles can both be up (S=+1), both down (S=-1), or 1 up/1 down (S = 0).
As stated, it must be in the singlet state. Electrons are fermions and obey the Pauli Exclusion principle, so the triplet state (where the electrons could both be up or down) is forbidden.
|
|  | jax
2005-12-05 19:21:26 | Just some additional info to help on this problem. The terms 'singlet', 'triplet' 'doublet' come from the multiplicity 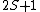 of the state. of the state.
So for states that we call singlets, 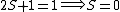 (as in this case when we have spin (as in this case when we have spin 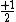 and and 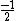 ) )
For doublets 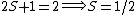 , etc. , etc.
agaliarept
2006-12-01 18:49:05 |
Thank you sir. Another needed post.
|
|  | astro_allison
2005-11-25 04:32:34 | is it fair to say that the gs will always be a spin singlet? (no matter the Z; He, H, Li, ...).
yosun
2005-11-26 01:44:48 |
astro_allison: if 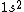 is a ground state, then it is a spin-singlet (see solution above for why). however, if is a ground state, then it is a spin-singlet (see solution above for why). however, if 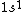 is a ground state, then it is not a spin singlet. So, in general, spin-singlet status depends on the number of electrons in a particular configuration... not sure what you mean by whether it's "fair"? is a ground state, then it is not a spin singlet. So, in general, spin-singlet status depends on the number of electrons in a particular configuration... not sure what you mean by whether it's "fair"?
|
|  | cakedamber
2005-11-11 22:22:50 | Sorry about the null post above, I was getting the hang of your interface. Anyhow, I'm sorry to say this, but your explanation above is flat-out wrong. The singlet state is when the total SPIN angular momentum is 0, i.e. when 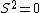 . You're absolutely right that in the . You're absolutely right that in the 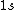 state, state, 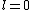 , but , but 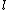 is ORBITAL angular momentum, not spin angular momentum, so that's irrelevant. The reason the ground state of helium must be a singlet is more complicated. Electrons are fermions, which means that the overall wavefunction for two electrons must be antisymmetric. In the ground state of helium, both electrons are in the same spatial state, meaning that their combined spatial wavefunction is symmetric. Therefore, in order to keep their overall combined wavefunction antisymmetric, their combined spin wavefunction must be antisymmetric -- meaning that they are in a spin singlet state, and thus (A) is the right answer. is ORBITAL angular momentum, not spin angular momentum, so that's irrelevant. The reason the ground state of helium must be a singlet is more complicated. Electrons are fermions, which means that the overall wavefunction for two electrons must be antisymmetric. In the ground state of helium, both electrons are in the same spatial state, meaning that their combined spatial wavefunction is symmetric. Therefore, in order to keep their overall combined wavefunction antisymmetric, their combined spin wavefunction must be antisymmetric -- meaning that they are in a spin singlet state, and thus (A) is the right answer.
yosun
2005-11-11 22:50:42 |
cakedamber: thanks for pointer; the solution has been updated.
|
cakedamber
2005-11-12 16:08:57 |
Nice. That's much better.
|
liuyuhang599
2017-04-04 14:43:16 |
Your answer is correct, 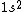 gives two possible states ( |+-> - |-+>) the singlet state, and ( |+-> +|-+> ) the triplet state. And because electron is fermion, only the antisymmetric singlet state is allowed. gives two possible states ( |+-> - |-+>) the singlet state, and ( |+-> +|-+> ) the triplet state. And because electron is fermion, only the antisymmetric singlet state is allowed.
|
|  | cakedamber
2005-11-11 22:14:41 | |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
