|
GR9277 #63
|
|
|
Problem
|
|
\prob{63}
Which of the following is true if the arrangement of an isolated thermodynamic system is of maximal probability?
- Spontaneous change to a lower probability occurs
- The entropy is a minimum
- Boltzmann's constant approaches zero.
- No spontaneous change occurs.
- The entropy is zero.
|
Statistical Mechanics }Maximal Probability }Maximal Probability
According to statistical mechanics, maximal probability is the sate of highest entropy---it's the peak of a Gaussian curve, the average score on a normally-curved test.
Spontaneous change to lower probability thus does not occur since maximal probability is the most stable state--one of highest entropy. Boltzmann's constant never approaches 0, however in the third law of thermodynamics, one has the entropy approaching 0 for  . .
Eliminating choices, one has choice (D).
|
|
|
Alternate Solutions |
QuantumCat
2014-09-16 14:50:15 | The key to answering this question by process of elimination is to remember that in an isolated thermodynamic system, entropy can NEVER decrease. B & E are eliminated. Boltzmann's constant is just that, a constant. C eliminated.
This leaves A & D. Of these two, you can (correctly) guess that a state of lower probability means a state of lower entropy; a transition to a state of lower probability (entropy) is prohibited in an isolated system. That leaves only D. |  |
|
|
Comments |
QuantumCat
2014-09-16 14:50:15 | The key to answering this question by process of elimination is to remember that in an isolated thermodynamic system, entropy can NEVER decrease. B & E are eliminated. Boltzmann's constant is just that, a constant. C eliminated.
This leaves A & D. Of these two, you can (correctly) guess that a state of lower probability means a state of lower entropy; a transition to a state of lower probability (entropy) is prohibited in an isolated system. That leaves only D.
QuantumCat
2014-09-16 14:57:33 |
Also, entropy does not go to 0 as T  0, but rather 0, but rather 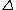 S S  0 so that the entropy remains close to constant and finite at temperatures approaching absolute zero. 0 so that the entropy remains close to constant and finite at temperatures approaching absolute zero.
|
|  | Naismith
2011-10-10 04:32:54 | I'm still confused, since my line of reasoning went like this: Most stable -> fine. But small random flutuations always occur, therefore a spontanous change to lower probability occurs, since we are at the highest probability anyway... |  | sdf
2010-09-06 17:02:56 | I respectfully disagree with ETS here. Quoting from Schroeder (p66) "any random fluctuations away from the most likely macrostate will be utterly unmeasurable." BUT THEY DO OCCUR! And were not talking about microstates here. The second law is only a probabilistic phenomenon, and probability says that if you wait long enough, every molecule roles snake eyes and ends up in one corner of the room. This question should read "system at its thermodynamic limit" because then spontaneous change would never occur and there is no room for interpretation. /sorry, rant over
erict
2010-10-02 03:50:11 |
I respectfully agree with you, and very disrespectfully disagree with ETS.
|
apps00
2010-10-06 10:21:42 |
I second that as well
|
flyboy621
2010-10-22 13:42:18 |
In my humble opinion your disagreement with ETS is a minor quibble. Clearly none of the other choices are remotely correct.
Sure, it might have been more correct to say "no MACROSCOPIC spontaneous change occurs." But choice D is pretty much the truth, while all of the other choices are patently false.
|
neon37
2010-11-12 04:13:59 |
maybe "isolated Thermodynamic system" means only concern yourself with macroscopic phenomenons only. Just a thought.
|
Limerick Jim
2011-11-04 19:10:01 |
ETS covers themselves in this situation really well "Choose the answer which is MOST correct". shitty but D is more correct than the others
|
|  | neutrinosrule
2008-10-04 18:12:00 | if you know nothing about thermo at all, you can at least realize that A and D are opposites... It is at max probability so either it changes to a lower probability or it doesnt. This means one of these two things has to happen and either A or D has to be correct. After that, a logical next thought may be: why would an isolated thermodynamic system spontaneously change? And if you thought it would make more sense for it not to change than to change, you would get the right answer.
Da Broglie
2011-04-07 17:00:11 |
Way to go! Exactly how I did it. No knowledge of stat mechanics or maximal probability needed.
|
|  | thebigshow500
2008-09-10 01:34:47 | "According to statistical mechanics, maximal probability is the state of highest entropy....since maximal probability is the most stable state--one of highest entropy." When the entropy reaches the highest, the energy state must become the most unstable, right? This sounds contradicting to me...And what does the probability refer to?
I have no idea about these concepts in Stat Mech. Is there any reference for us to study the "Maximal Probability"?
Lukav
2008-10-04 11:52:45 |
The probability is referring to the likelihood of finding the system in that particular state (given an ensemble of systems). Which is a Gaussian having its peak at the highest entropy. Entropy always tends to be increasing (imagine ice melting). I guess the wording 'becoming more random' might make a little more sense than 'becoming more unstable'
This is taken from a wiki article:
"The macroscopic state of maximal entropy for the system is the one in which all micro-states are equally likely to occur..."
|
neon37
2008-10-21 00:29:12 |
So we know, entropy, ) where where 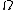 is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable. is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable.
|
neon37
2008-10-21 01:14:12 |
So we know, entropy, ) where where 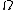 is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable. is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable.
|
neon37
2008-10-21 01:19:12 |
So we know, entropy, ) where where 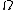 is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable. is the multiplicity. Maximum entropy means maximum multiplicity. Maximum multiplicity implies maximum probability for that macrostate to occur. Thus, most stable.
|
adjwilley
2009-11-04 09:16:08 |
So let's say that the system reaches the state of absolute highest entropy, or the most probable state. Then random changes occur, like they always do. It can't stay in that most probable state forever. There will be random (albeit small) fluctuations to states of lower entropy. Thus, (A).
|
kroner
2009-11-04 23:49:33 |
Saying the system is in the state of highest entropy is a description of the macroscopic state of the system. That single macroscopic state includes many possible microscopic states. The system fluctuates over time between various micro states in that set, but the macro state can never be said to spontaneously change to one of lower entropy. That's precisely the second law of thermodynamics.
|
sree
2011-11-17 02:58:18 |
I THINK STABLE STATE IS NOT ACTUALLY THE STATE AT WHICH ENTROPY IS MAXIMUM, BUT A STATE AT WHIC ENTROPY AND GIBBS FREE ENERGY IS BALANCED, SYSTEM TRIES TO HAVE HIGHEST ENTROPY POSSIBLE AND LOWEST FREE ENERGY, SINCE THESE PARAMETERS ARE OPPOSITE IT HAS TO BALANCE IN BETWEEEN
|
|  | Andresito
2006-03-28 20:24:09 | "state" in first line |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
