|
GR9277 #68
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mpdude8
2012-04-20 00:31:36 | Even though there's nothing that says a telescope cannot have mirror sizes to the order of ~ 1m, this is unreasonable for the GRE. I've found that the GRE mostly asks physically relevant/"real", reasonable examples. Imagine putting your eye up to such a telescope -- would a telescope of diameter 1mm, 1cm 1m, or 100m be reasonable?
Again, not a physically good solution whatsoever, but when you're trying to crank out answers, this strategy will allow you to narrow down ridiculous answers.
ykwvn
2015-10-20 19:07:59 |
I would be more careful in what you decide to be unreasonable in this question. A 1m telescope is not at all unreasonable, its a fairly modest sized research telescope, the ELT has a 40m diameter. Not all telescopes are ones that you would put your eye up to.
|
|  | Tbot
2011-10-25 15:47:22 | This is a total shot in the dark for me, but this is how I did it, and it gave me the right answer...
I figure the "angular separation" refers to the arc length on the mirror that separates light from the stars. This arc length needs to be at least on the order of a wavelength to allow the two sources to be distinguished.
This gives 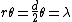 . Plugging in numbers gives a diameter of about 13 cm. That is closest to the correct answer C. . Plugging in numbers gives a diameter of about 13 cm. That is closest to the correct answer C. |  | heypete
2010-11-05 17:23:09 | Also, just some sanity checks: a telescope of 1mm, 1cm, or 100m doesn't make much sense. Those simply aren't terribly realistic values for optical telescopes (though 100m+ telescopes are not uncommon for radio).
10cm and 1m are "reasonable" values for telescope diameters. 10cm ones are not uncommon for amateur telescopes, and 1m-class telescopes are at the low range for research telescopes (I do some research with a 1.55m telescope). Seems plausible.
Even if one didn't know anything about diffraction, knowing a bit about reasonable sizes for telescopes can simplify the problem down to two possible answers, rather than 5.
neon37
2010-11-12 04:55:37 |
100 m telescope is not unreasonable anymore. Various concepts of 100 m telescope have surfaced already, such as OWL by ESO. Besides 30m telescope is already in its design and development phase.
|
|  | tan
2009-10-31 04:48:19 | Plugging in the numbers gives a, not c. What's wrong?
pkamal
2010-10-03 14:23:29 |
Remember that 1 micrometer=10^-6 m not 10^-3 m.
|
|  | justguessing
2009-09-29 08:13:27 | I always used that formula in degrees, not rad. I'm confused.
myscifilullaby
2012-04-03 14:49:08 |
use rads to make the units right. rads are a "unitless unit" i.e. a ratio between two lengths (the radius and circumpherence of a circle) so meters/rads gives meters while meters/degrees gives... not meters
|
|  | ramparts
2009-08-06 21:08:19 | If you (like many people!) don't have this formula memorized, there's really only one logical way (dimensionally) to get the answer, and that's to divide the wavelength by the angle. Unless there's a dimensionless constant that's not on the order of 1 (in this case, it's 1.22, which is great), that'll give you a rough and easy order of magnitude estimation in cases like this, where the answers are off by powers of 10. |  | p3ace
2008-05-11 15:32:40 | So why do we use the formula for diffraction to get the width of a mirror for resolution????
hot_dark_matter
2008-05-23 15:19:11 |
We use the concept of diffraction because when any light interacts with an optical instrument, the light diffracts. When two sources have a small angular separation, the central maxima of their respective diffraction patterns can overlap; thereby making two sources look like one.
To visualize the phenomena, consider a monochromatic source shining on a single slit and producing a diffraction pattern. Now if a second, identical source is turned on at the same position, the patterns overlap and an observer cannot discern whether there are one or two sources. If the second source is moved to one side, the second diffraction pattern appearing on the screen is also displaced.
To observe two distinct patterns we essentially need the central max of one pattern to occur, at the very least, at the first minima of the other pattern. Since the first minima occurs at 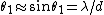 , the angular separation of the two sources must also be about , the angular separation of the two sources must also be about 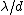 . As mentioned previously, the 1.22 is a numerical factor having to do with circular geometry rather than 1-D slits. . As mentioned previously, the 1.22 is a numerical factor having to do with circular geometry rather than 1-D slits.
|
student2008
2008-10-16 06:00:00 |
This is called the Rayleigh criterion.
See also http://en.wikipedia.org/wiki/Angular_resolution
|
|  | hamood
2007-04-04 16:48:52 | Can anyone please tell me where the factor of 1.22 comes from, like how do we derive the formula. just curious about it....
nigelfordham
2007-04-10 12:22:21 |
the 1.22 comes from the evaluated bessel function in the derivation of diffraction of a circular aperture.
http://cnx.org/content/m13097/latest/
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
