|
GR9277 #75
|
|
|
|
|
Alternate Solutions |
nitin
2006-11-20 08:46:22 | Conservation of momentum:
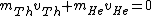 , ,
since Uranium atom decays at rest.
This implies that
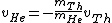 . .
The kinetic energy of the He atom is:
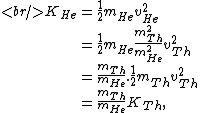
where 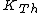 is the kinetic energy of the Th atom. The answer (E) follows. is the kinetic energy of the Th atom. The answer (E) follows. |  | kevglynn
2006-10-04 10:54:32 | A good and simple solution:
Since we know that each products' momentums are identical, we can then use the relation K=(p^2)/2m (a manipulation of .5mv^2).
Since p^2 is identical for each product, we need only look at what we're dividing p^2 by. Since Thorium has a greater mass, it's kinetic energy will be smaller.
hope it helps (and sorry for ending a sentence in a preposition ;-))
kevglynn
2006-10-04 10:55:43 |
Sorry, I forgot to say, that my solution also points to answer E as the correct response.
|
|  |
|
|
Comments |
mpdude8
2012-04-20 00:45:52 | Reasoning + one bit of physics (conservation of momentum) can solve this.
A and B are eliminated because they essentially say the same thing. Also, if both products have the same momentum after decaying, the smaller mass must have the higher velocity. This also eliminates D, and confirms E as the correct answer.
h.fei10
2012-11-05 00:43:03 |
I agree with you, since kinetic energy is mv^2) , which can be viewed as , which can be viewed as pv) . When momentum is conserved, the smaller mass object always have higher kinetic energy. By the way, I ignore the relativistic effects. . When momentum is conserved, the smaller mass object always have higher kinetic energy. By the way, I ignore the relativistic effects.
|
|  | mike
2009-11-04 13:18:16 | I "think" this can be solved by elimination:
The uranium nucleus is initially at rest. So initially, there is no momentum. Using this fact repeatedly:
A: No reason to believe the decay is 'elastic', in the sense of a collision. Any knowledge of binding energy eliminates this...
B: Can't be true by conservation of momentum. They must have the same magnitude of momentum, and they both do not have the same mass.
C: Again, violates conservation of momentum. They have to go in opposite directions.
D: Their momenta must be equal, so again this can't be true.
E: Only thing left.
natec
2013-09-03 11:25:21 |
that's exactly how I solved it.
|
|  | Furious
2007-10-29 18:57:28 | I'm not sure if this is valid or not, but I got this problem right by thinking about potential vs. kinetic.
The Uranium nucleus is at rest, meaning all of its energy is contained in the potential of the binding energy.
Now you look at the Thorium and the Helium, and realized that Thorium will have a huge binding energy, and Helium won't even have a binding energy, since Kinetic energy has a quadratic dependence on velocity and a linear on mass, it stands to reason, that most of Thorium's energy will still be potential in its binding energy, while all of the heliums energy will be kinetic.
I'm not sure if I'm making incorrect assumptions but that all makes sense to me, and it leaves out formulas (which I consider to be a benefit) |  | nitin
2006-11-20 08:46:22 | Conservation of momentum:
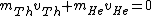 , ,
since Uranium atom decays at rest.
This implies that
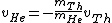 . .
The kinetic energy of the He atom is:
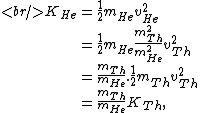
where 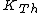 is the kinetic energy of the Th atom. The answer (E) follows. is the kinetic energy of the Th atom. The answer (E) follows.
motek
2008-10-13 10:23:13 |
This is a non-relativistic calculation. Is it valid?
|
flyboy621
2010-10-22 17:03:57 |
All we need to know is that since momentum must be conserved, the two nuclei must have equal and opposite momentum. Therefore the one with smaller mass must have greater speed and hence more kinetic energy.
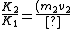 v_2}{(m_1 v_1) v_1}=\frac{v_2}{v_1})
Even if there is some relativistic correction, it won't affect which particle has the greater kinetic energy.
|
|  | kevglynn
2006-10-04 10:54:32 | A good and simple solution:
Since we know that each products' momentums are identical, we can then use the relation K=(p^2)/2m (a manipulation of .5mv^2).
Since p^2 is identical for each product, we need only look at what we're dividing p^2 by. Since Thorium has a greater mass, it's kinetic energy will be smaller.
hope it helps (and sorry for ending a sentence in a preposition ;-))
kevglynn
2006-10-04 10:55:43 |
Sorry, I forgot to say, that my solution also points to answer E as the correct response.
|
Mexicana
2007-10-04 18:11:50 |
This is a veeery nice solution indeed. You save a lot of algebra had you done it the way nitin is showing.
|
laxatives
2012-08-08 07:46:34 |
i'm confused, how do you know that the thorium and helium products have the same momentum?
|
laxatives
2012-08-08 07:47:50 |
Nevermind, forgot the uranium was initially at rest
|
|  | snimi1
2005-11-11 05:44:14 | The answer is (E). The momentum and energy are conserved in this process. From momentum conservation we know that the speed of He (with mass m) will be bigger than the speed of Th (with mass M) by a factor of M/m.
Thus the kinetic energy of He will be larger than the kinetic energy of Th
Andresito
2006-03-29 10:37:39 |
I agree, thank you for posting it.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
