|
GR9277 #78
|
|
|
Problem
|
|
\prob{78}
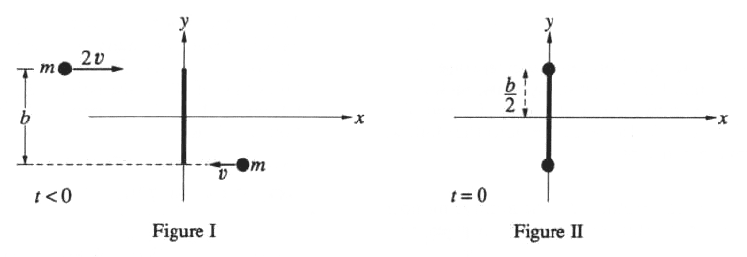
One ice skater of mass m moves with speed 2v to the right, while another of the same mass m moves with speed v toward the left, as shown in Figure I. Their paths are separated by a distance b. At t=0, when they are both at x=0, they grasp a pole of length b and negligible mass. For t>0, consider the system as a rigid body of two masses m separated by distance b, as shown in Figure II. Which of the following is the correct formula for the motion after t=0 of the skator initially at y=b/2?
-
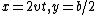
-
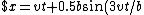, \;\;y=0.5b\cos(3vt/b)$)
-
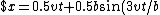, \;\;y=0.5b\cos(3vt/b)$)
-
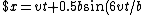, \;\;y=0.5b\cos(6vt/b)$)
-
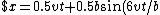, \;\;y=0.5b\cos(6vt/b)$)
|
Mechanics }Multiple Particles }Multiple Particles
The angular momentum equation gives the angular frequency. 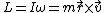 , which relates the angular momentum to the moment of inertia, the angular velocity, the radius of gyration and the linear velocity. , which relates the angular momentum to the moment of inertia, the angular velocity, the radius of gyration and the linear velocity.
The system spins about its center of mass, which is conserved. Since the pole is massless and the skaters are off the same mass, 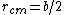 . The moment of inertia of the system is just . The moment of inertia of the system is just 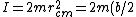^2) . .
Thus, the angular momentum equation gives 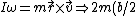^2 \omega =m b/2 (v + 2v) \Rightarrow 2(b/2) \omega = 3v \Rightarrow \omega = 3v/b) , since the cross-products point in the same direction. Now that one has the angular velocity, one eliminates all but choices (B) and (C). , since the cross-products point in the same direction. Now that one has the angular velocity, one eliminates all but choices (B) and (C).
Now, take the time-derivative of x for choices (B) and (C), then evaluate it at 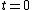 . .
For B, one has 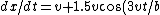 \rightarrow 2.5v) for for 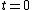 . .
For C, one has 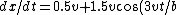 \rightarrow 2v) for for 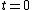 . .
Since the top skater is initially at =2v) , only choice (C) has the right initial condition. Choose choice (C). , only choice (C) has the right initial condition. Choose choice (C).
(FYI: The center of mass velocity is given by 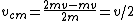 . One can also arrive at (C) by noting conservation of center of mass velocity, since there is no net force.) . One can also arrive at (C) by noting conservation of center of mass velocity, since there is no net force.)
|
|
|
Alternate Solutions |
huanghandage
2019-04-04 20:27:28 | We know that the thing is gonna rotate, so eliminate A. Take the derivative of the five solutions, then x\'(0) has to be 2v, so eliminate B, D, and E, and the only choice left is C. |  | Niko
2010-11-11 21:47:06 | Throw out E because you know the thing is going to rotate.
One should notice that at t=0 the x-component of the velocity should be 2v.
Take the time derivative of all of the answers (shouldn't take more than 30s) and realize that only c satisfies.
Good rule of thumb:
When you have to choose the correct relation from a set of equations always look at the limits and initial conditions. Applying this and dimension analysis usually eliminates 2 or more of the choices. |  | flyboy621
2010-10-22 20:58:00 | There are 2 conserved quantities here: linear momentum and angular momentum.
Conservation of linear momentum tells us that the CM moves at the same velocity after the "collision" as before, namely
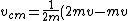=\frac{v}{2})
so it must be (C) or (E). To narrow it down, we need to find the frequency 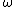 . Conservation of angular momentum (about the center of the rod) says . Conservation of angular momentum (about the center of the rod) says
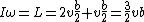
But 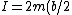^2=mb^2/2)
which gives 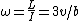 , as in answer (C). , as in answer (C). |  |
|
|
Comments |
DillonB
2019-05-23 17:57:48 | Wowzers, I should\'ve listened and paid more attention in high school physics class.. I\'m now in evening university classes learning physics and it still seems way over my head, please help! Dillon - www.drivingschoolwinnipeg.com |  | huanghandage
2019-04-04 20:27:28 | We know that the thing is gonna rotate, so eliminate A. Take the derivative of the five solutions, then x\'(0) has to be 2v, so eliminate B, D, and E, and the only choice left is C. |  | livieratos
2011-11-09 04:38:54 | can someone explain why I = 2m(b/2)^2 please?
neo55378008
2012-08-18 11:44:18 |
I = 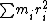 by definition by definition
|
netphysics
2012-11-01 19:02:11 |
and it is the moment of inertia of c.m.
|
|  | Niko
2010-11-11 21:47:06 | Throw out E because you know the thing is going to rotate.
One should notice that at t=0 the x-component of the velocity should be 2v.
Take the time derivative of all of the answers (shouldn't take more than 30s) and realize that only c satisfies.
Good rule of thumb:
When you have to choose the correct relation from a set of equations always look at the limits and initial conditions. Applying this and dimension analysis usually eliminates 2 or more of the choices.
kap09c
2013-10-17 18:33:09 |
I think you mean A, and no, it should be .5 v ...
|
NoPhysicist3
2017-03-23 13:29:00 |
yes, he should have said \"throw out A\"\r\nwhy would it be o.5? It is 2.
|
|  | Niko
2010-11-11 21:46:27 | Throw out E because you know the thing is going to rotate.
One should notice that at t=0 the x-component of the velocity should be 2v.
Take the time derivative of all of the answers (shouldn't take more than 30s) and realize that only c satisfies.
Good rule of thumb:
When you have to choose the correct relation from a set of equations always look at the limits and initial conditions. Applying this and dimension analysis usually eliminates 2 or more of the choices. |  | flyboy621
2010-10-22 20:58:00 | There are 2 conserved quantities here: linear momentum and angular momentum.
Conservation of linear momentum tells us that the CM moves at the same velocity after the "collision" as before, namely
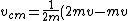=\frac{v}{2})
so it must be (C) or (E). To narrow it down, we need to find the frequency 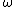 . Conservation of angular momentum (about the center of the rod) says . Conservation of angular momentum (about the center of the rod) says
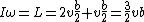
But 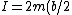^2=mb^2/2)
which gives 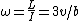 , as in answer (C). , as in answer (C).
dc771957
2016-10-18 23:36:59 |
Hey, I think you dropped your \'m\' terms in where you first calculated the angular momentum as r x p. You kept the \'m\'s in your moment of inertia term, and you need them in the angular momentum jaunt to cancel out. \r\n\r\nGreat solution btw.
|
|  | wikiwert
2010-09-30 07:36:30 | I am afraid the GRE solution is wrong. The w in yosunīs solution is the angular velocity "with respect to the center of mass". It is the angular speed about the rotation axis of a rigid body ( L = I * w with I the moment of inertia tensor). But some may not be very familiarized with this Classical Mechanics result; so just consider the center of mass (CM) frame.
Velocities are 3/2 * v and - v/2 in the CM frame. In this system there is only rotation (the CM does not move); this should make clear that the following result will be correct. Angular momentum is conserved and it is initially 3/2 *v * m * b/2 + 1/2 * v * m * b/2 = m * b * v. And in this system (CM does not move) is that we have L = I * w. As I = 2 * m * (b/2)^2, we have that w = 2 * v/b.
Transforming to the original system, a v/2 * t term has to be added to the x ( t ) term.
wikiwert
2010-10-01 19:16:44 |
Ignore the previous comment. I donīt know if any body is modertaing the comments any longer...but please erase the previous one. I thought it was very strange that the GRE solution was wrong...but it wasnīt until I told somebody how I solved the problem, that I realized I calculated -v+v/2 and not -v -v/2 : P. Sorry.
|
|  | Ning Bao
2008-01-30 07:31:32 | I don't think it needs to be that complicated: this is more of a boundary values problem.
Taking derivatives of everything immediately eliminates all but A and C, as v(0)=2v in the x direction. A fails because there is no reason for the y-coordinate to stay fixed. Thus, C.
flyboy621
2010-10-22 18:31:51 |
Sorry, but I don't think this comment makes sense at all, except that it's true that y can't be constant.
|
liliapunto
2013-07-15 15:44:46 |
Ning makes total sense and this is the easiest method.
|
|  | mygoldfleece
2007-11-01 02:44:07 | Why does the energy conserve?
Instead of energy conservation, I use angular momentum conservation (with reference point at (0,-b/2)) |  | lambda
2007-10-21 21:46:06 | I did it a simpler way than the official solution, although not as quick as Richard's solution.
The center of mass of the two masses will travel to the right with a velocity 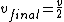 through conservation of linear momentum (the same way Richard got it). So the expression for through conservation of linear momentum (the same way Richard got it). So the expression for  will have a will have a 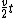 term. term.
The angular velocity 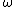 is calculated through conservation of energy: is calculated through conservation of energy:
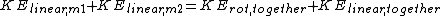
With more math,
^{2}+\frac{1}{2}mv^{2}=\frac{1}{2}I\omega^{2}+\frac{1}{2}(2m)(\frac{v}{2})^{2}) , ,
where the moment of inertia 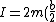^{2}) . . |  | Richard
2007-09-16 22:53:32 | This problem doesn't have to be complicated.
You need to know two things: the linear velocity and the angular velocity.
The linear velocity is easily obtained by conservation of momentum:
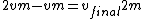
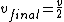
The angular velocity is almost as easy. Note that
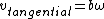
The tangential velocity is the sum,  , since both contribute to rotation acting at the poles in opposite directions: , since both contribute to rotation acting at the poles in opposite directions:
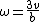
 and and 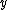 are out of phase by are out of phase by 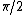 . .
The answer is C.
lambda
2007-10-21 21:28:08 |
I'm not really seeing why the tangential velocity of the two masses together is equal to the sum of their original linear velocities. Why can they be added this way?
|
sblmstyl
2008-09-23 16:16:11 |
shouldn't 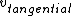 = = 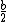 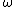 ? ?
|
Albert
2009-10-21 11:21:44 |
Yes, V(tangential) should be (b/2)*w since the radius is b/2 not b.
|
cbb6x2
2010-11-08 22:42:43 |
Why doesn't it work when you use velocity=b/2*omega? You would get (E) as the answer using this method
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
