|
GR9677 #19
|
|
|
|
|
Alternate Solutions |
fjornada
2009-10-19 10:11:53 | Yet another solution with energy conversion (using atomic systems). If you are used to working with atomic physics, it'll be quite quick, otherwise forget this post.
In atomic systems, energy is given by Hartree, distance by Bohr, and the best, 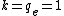 . .
One Hartree is twice the ground state of the H atom, so divide 5 Mev by 27 eV and you'll get the kinetic energy in a.u. Also, in a.u. 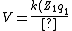(Z_2 q_2)}{r}= \frac{100}{r}) . .
Now make T=V and you'll find r ~ 5 E-4 Bohrs. One Bohr is the classical electron orbit (~ 5E-11 m). A rough guess around one Angstrom (1E-10 m) works just fine.
|  | wittensdog
2009-10-16 18:32:09 | There is a way to do this without ever making explicit reference to the conversion between electron-volts and joules. Remember that an electron-volt is exactly what it sounds like, the electron charge multiplied by one volt. If you divide 1 eV by the electron charge, you have one volt, which is very nice because that is just 1 N * m / C , which is something that has a value of 1 in SI units.
Now, due to the col0umb potential, you're going to have a term of the form,
100 e^2 / ( 4 * pi * eps_0 * r )
on one side, and a term of the form,
E = 5 * 10 ^6 eV
on the other. So, what you can do is just divide by the electron charge, and get,
5 * 10^6 V = 100 e / (4 * pi * eps_0 * r)
The electron charge and eps_o are given on the front sheet, so now you just plug in numbers.
By dividing out the electron charge, you're basically working with electric potential, and not potential energy. |  | kcme
2007-06-17 10:25:20 | I would rather solve this with dimensional analysis. No calculations necessary
You know to be backscattered at such a large angle, the distance of closest approach is going to be very small, on the order of the size of the nucleus (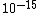 ). That eliminates choices C, D, and E. ). That eliminates choices C, D, and E.
So what about A? Well, 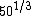 is somewhere between 3 and 4, so at most choice A is something like 1.22*4 fm, or about 5 fm. That's smaller than a big nucleus like silver. is somewhere between 3 and 4, so at most choice A is something like 1.22*4 fm, or about 5 fm. That's smaller than a big nucleus like silver.
That leaves choice B, which at 29 fm strikes me as quite reasonable |  |
|
|
Comments |
arturodonjuan
2016-10-17 16:50:10 | There\'s a really nifty alternative to just \"plugging in the constants\" from the front page, which is all quite complicated. This requires remembering 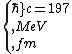 and and 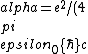) , where , where 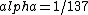 is the fine-structure constant.\r\n\r\nThe equation we\'re solving, which you should be able to write down in a millisecond, is (by conservation of energy),\r\n\r\n is the fine-structure constant.\r\n\r\nThe equation we\'re solving, which you should be able to write down in a millisecond, is (by conservation of energy),\r\n\r\n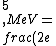(50e)}{4\\pi\\epsilon_0 d}) \r\n\r\nor, moving \r\n\r\nor, moving 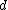 to the other side,\r\n\r\n to the other side,\r\n\r\n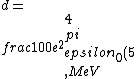}) \r\n\r\nas you can see, \r\n\r\nas you can see, 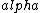 has popped out,\r\n\r\n has popped out,\r\n\r\n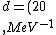\\left(\\frac{e^2}{4\\pi\\epsilon_0}\\right)) \r\n \r\n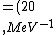(\\hbar c \\alpha)) \r\n \r\n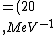\\left(197\\,MeV\\,fm\\right)\\left(\\frac{1}{137}\\right)) \r\n \r\n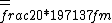 \r\n \r\n \r\n \r\n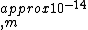 \r\n\r\nThis is a hell of a lot easier to deal with. \r\n\r\nThis is a hell of a lot easier to deal with.
arturodonjuan
2016-10-17 16:51:15 |
Oh my f***ing gosh this doesn\'t display at all like the preview did.
|
|  | pam d
2011-09-11 19:21:18 | Okay so the scattering angle of 180 degrees was just a bunch of smoke and mirrors hiding a simple conservation of energy freebie. FFFFFFFUUUUUUUUUUUU
justin_l
2013-10-18 00:26:21 |
well technically the 180 degrees was what told you you could directly apply conservation of energy. It means it was a head-on collision.
|
|  | walczyk
2011-04-03 02:22:02 | You all should remember J/eV is 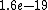 which is equal to the charge of an electron q!! That should make this problem SO easy if you remember k is nearly which is equal to the charge of an electron q!! That should make this problem SO easy if you remember k is nearly 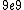 |  | Phys4
2010-08-03 16:50:03 | If you set up the problem correctly like Yosun does, just do an order of magnitude calculation. You will get -14 and one can plainly see the other solutions have at least two orders of magnitude off. The small coefficients indicate that one does not have to worry about them influencing the order of magnitude. |  | fjornada
2009-10-19 10:11:53 | Yet another solution with energy conversion (using atomic systems). If you are used to working with atomic physics, it'll be quite quick, otherwise forget this post.
In atomic systems, energy is given by Hartree, distance by Bohr, and the best, 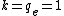 . .
One Hartree is twice the ground state of the H atom, so divide 5 Mev by 27 eV and you'll get the kinetic energy in a.u. Also, in a.u. 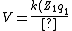(Z_2 q_2)}{r}= \frac{100}{r}) . .
Now make T=V and you'll find r ~ 5 E-4 Bohrs. One Bohr is the classical electron orbit (~ 5E-11 m). A rough guess around one Angstrom (1E-10 m) works just fine.
|  | wittensdog
2009-10-16 18:32:09 | There is a way to do this without ever making explicit reference to the conversion between electron-volts and joules. Remember that an electron-volt is exactly what it sounds like, the electron charge multiplied by one volt. If you divide 1 eV by the electron charge, you have one volt, which is very nice because that is just 1 N * m / C , which is something that has a value of 1 in SI units.
Now, due to the col0umb potential, you're going to have a term of the form,
100 e^2 / ( 4 * pi * eps_0 * r )
on one side, and a term of the form,
E = 5 * 10 ^6 eV
on the other. So, what you can do is just divide by the electron charge, and get,
5 * 10^6 V = 100 e / (4 * pi * eps_0 * r)
The electron charge and eps_o are given on the front sheet, so now you just plug in numbers.
By dividing out the electron charge, you're basically working with electric potential, and not potential energy.
wittensdog
2009-10-16 18:43:46 |
So I guess the broader moral is that whenever you have an expression that has the electron charge, and also units of eV in it, you can pull the electron charge out from the term " eV " in order to make things simpler.
|
flyboy621
2010-10-23 06:54:13 |
This is the best solution.
|
dmerthe
2011-11-09 22:08:03 |
I like this solution. Simple and easy to remember.
|
|  | physicsisgod
2008-10-28 15:21:50 | Yosun's solution is right, but if you're like me and want to know the physics behind this, check this out:
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/rutsca2.html#c5
Maybe the other commenters already knew this, but this question is asking about Rutherford scattering, which is actually much more detailed and interesting than the solution suggests. ETS was just nice and gave us a 180 degree scattering angle, which simplifies things quite a bit. In fact, if you recognize this as Rutherford scattering at 180 degrees, you can just memorize the formula 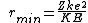 when the angle is 180 degrees,. and get the right answer exactly. when the angle is 180 degrees,. and get the right answer exactly. |  | glkjap2
2008-06-11 01:24:35 | Quick way: The first thing we recall is that m_{\alpha}>>T so we can say 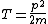 . Alpha particle has four nucleons each with approximately 940 MeV mass so we can approximate that . Alpha particle has four nucleons each with approximately 940 MeV mass so we can approximate that 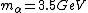 . So we find that approximately . So we find that approximately 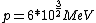 . Plugging 2p into the uncertainty relation we have . Plugging 2p into the uncertainty relation we have 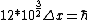 . Using . Using 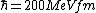 we find that we find that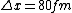 which is closest to answer B. which is closest to answer B. |  | kcme
2007-06-17 10:25:20 | I would rather solve this with dimensional analysis. No calculations necessary
You know to be backscattered at such a large angle, the distance of closest approach is going to be very small, on the order of the size of the nucleus (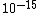 ). That eliminates choices C, D, and E. ). That eliminates choices C, D, and E.
So what about A? Well, 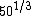 is somewhere between 3 and 4, so at most choice A is something like 1.22*4 fm, or about 5 fm. That's smaller than a big nucleus like silver. is somewhere between 3 and 4, so at most choice A is something like 1.22*4 fm, or about 5 fm. That's smaller than a big nucleus like silver.
That leaves choice B, which at 29 fm strikes me as quite reasonable
Moush
2010-09-29 19:09:21 |
I don't see how simply being reflected 180 degrees means that an extremely close nuclear approach is involved. Sure, if 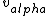 << << 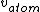 then it's more likely that it gets deflected < 180 degrees. But if then it's more likely that it gets deflected < 180 degrees. But if 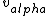 < < 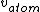 or or 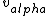 ~/>/>> ~/>/>> 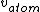 then 180 deg reflections are likely. Proximity will be inversely proportional to its speed and probability will be directly proportional to its speed. then 180 deg reflections are likely. Proximity will be inversely proportional to its speed and probability will be directly proportional to its speed.
I guess getting to know ETS is part of the problem, knowing when to assume and how much one can without much worry...
|
|  | cyberdeathreaper
2007-01-07 21:25:35 | I second that comment by scottopoly - this seems like a very involved calculation to be doing by hand (translation = it seems time-consuming). Are there any shortcuts in the calculation to consider? Or, perhaps another approach?
yosun
2007-02-22 19:04:19 |
Well, it's not very time consuming, since we are just solving for r... From baby's basic math, you should get 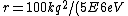\approx100\times 9E9\times 1.5E-19/(5E6) ) . Note that in the approx, I did not square the q, since one of the q's cancel in the conversion . Note that in the approx, I did not square the q, since one of the q's cancel in the conversion 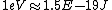 ... The answer comes out to the right order, which is enough for this question. ... The answer comes out to the right order, which is enough for this question.
|
|  | scottopoly
2006-11-03 15:49:25 | ah yes, the old "convert to SI".
Blake7
2007-09-22 22:06:35 |
eV to Joules and back is given no less than TWICE in the Table of Information at the beginning of the test.
You should easily see it in Planck's constant
h = 6.63E-34 Joule*second = 4.14E-15 eV* second
(6.63E-34Joule = 4.14E-15 eV)
and also again in the magnitude of the electron charge
e = 1.6o218 E-19 Coulomb
(from the definition of "Electron Volt")
Drill those a couple of times and they'll be right there for you.
|
|  |
|
| Post A Comment! |
You are replying to:
There is a way to do this without ever making explicit reference to the conversion between electron-volts and joules. Remember that an electron-volt is exactly what it sounds like, the electron charge multiplied by one volt. If you divide 1 eV by the electron charge, you have one volt, which is very nice because that is just 1 N * m / C , which is something that has a value of 1 in SI units.
Now, due to the col0umb potential, you're going to have a term of the form,
100 e^2 / ( 4 * pi * eps_0 * r )
on one side, and a term of the form,
E = 5 * 10 ^6 eV
on the other. So, what you can do is just divide by the electron charge, and get,
5 * 10^6 V = 100 e / (4 * pi * eps_0 * r)
The electron charge and eps_o are given on the front sheet, so now you just plug in numbers.
By dividing out the electron charge, you're basically working with electric potential, and not potential energy.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
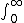 |
| $\partial$ |
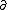 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
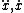 |
| $\sqrt{z}$ |
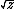 |
| $\langle my \rangle$ |
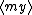 |
| $\left( abacadabra \right)_{me}$ |
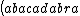_{me}) |
| $\vec{E}$ |
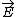 |
| $\frac{a}{b}$ |
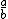 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
