|
GR9677 #32
|
|
|
|
|
Alternate Solutions |
jmason86
2009-09-26 14:08:10 | The pGRE is largely about answering problems quickly. Use MOE (method of elimination), order of mag, and physical intuition whenever possible.
KE = 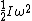 so a ratio of KE will just be a ratio of moment of inertia (I) since so a ratio of KE will just be a ratio of moment of inertia (I) since 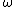 is fixed. is fixed.
Your physical intuition should tell you that the axis through the center will have a low I and an axis through any of the edges will have a larger I. Therefore, the ratio must be greater than 1. Eliminate (C) (D) (E).
Now you just need to know if it is going to be 2 or 3 times more KE (or I). As others have stated below, there are 3 masses that are not POINT masses, so any calculation you do will involve 3m, not 2. Eliminate (B) |  | yipee
2007-09-15 17:39:34 | I think the solution here is completely wrong. For moment of inertia about A, Ia=3*(1/3)mr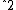 , where r is as shown in the above solution. So, then Ia=(1/3)ml , where r is as shown in the above solution. So, then Ia=(1/3)ml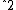 . Then, moment of inertia about B, Ib=0 + (1/3)ml . Then, moment of inertia about B, Ib=0 + (1/3)ml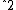 + (1/3)ml + (1/3)ml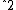 =(2/3)ml =(2/3)ml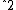 , where the zero comes from the mass at B. So, dividing the Kb by Ka then gives Ib/Ia = 2 as expected. , where the zero comes from the mass at B. So, dividing the Kb by Ka then gives Ib/Ia = 2 as expected. |  |
|
|
Comments |
kaic
2013-10-15 11:40:29 | If we call the distance from point A to each mass 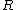 , then we can immediately think of the total inertia as three point masses at distance , then we can immediately think of the total inertia as three point masses at distance 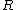 . .
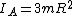
For B, one of the masses is at the center of gyration, so it doesn't contribute. We have two point masses at distance 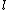 . .
Apply some basic trig to find the relation between 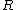 and and 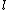 , ,
 = \frac{l/2}{R} = \frac{\sqrt{3}}{2})
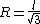
plug back into 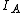 to find to find
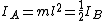
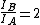
as in answer (B) |  | rachkov
2013-09-01 15:07:10 | On the GRE, it is important to go fast. While the original solution is good, here is a faster alternative:
You know that you need to look at the ratio of moments of inertia, mainly: 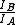 . .
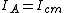 , which goes something like , which goes something like 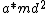 , where a is some positive constant you want to know and d is the distance between A and one of the masses. , where a is some positive constant you want to know and d is the distance between A and one of the masses.
md^{2}) from parallel axis theorem from parallel axis theorem
so the ratio ends up being: 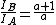
The only answer satisfying this condition is B) |  | w24729695
2012-11-08 06:27:53 | Ia=3mr^2 ,since 3^0.5=l, we can get Ia=ml^2
now when you move to point B, what you need is to calculate another inertia, thus Ib=0+ml^2+ml^2=2ml^2
2ml^2/ml^2=2 |  | gravity
2010-11-04 03:13:43 | I preferred another way.
Obviously,
I = 2ml = 2ml
The only hard part is figuring out the distance from A to each mass. I just guessed .6l.
So,
I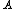 = 3m(.6l) = 3m(.6l)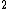 = ml = ml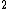
And the ration between these is 2. |  | sullx
2009-11-04 21:43:26 | For speed, I just though of it as a hoop (and probably because of the hoop hanging from a nail problem a few pages back).
For a hoop 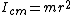 . Using the parallel axis theorem for the edge of the hoop yields . Using the parallel axis theorem for the edge of the hoop yields 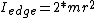 . .
Thus 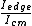 = 2/1 = 2/1 |  | jmason86
2009-09-26 14:08:10 | The pGRE is largely about answering problems quickly. Use MOE (method of elimination), order of mag, and physical intuition whenever possible.
KE = 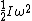 so a ratio of KE will just be a ratio of moment of inertia (I) since so a ratio of KE will just be a ratio of moment of inertia (I) since 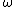 is fixed. is fixed.
Your physical intuition should tell you that the axis through the center will have a low I and an axis through any of the edges will have a larger I. Therefore, the ratio must be greater than 1. Eliminate (C) (D) (E).
Now you just need to know if it is going to be 2 or 3 times more KE (or I). As others have stated below, there are 3 masses that are not POINT masses, so any calculation you do will involve 3m, not 2. Eliminate (B)
Dx2wUV
2009-10-06 13:30:52 |
If you eliminate B then you eliminate the correct answer, according to ETS
|
dogsandfrogs
2009-10-07 14:12:42 |
Eliminate (B)? But B is the answer...
|
mrTrig
2010-10-23 13:09:01 |
You probably dont want to eliminate (B) since (B) is the answer.
|
KLS
2013-10-12 13:33:52 |
The answer key states that (B) is the correct answer, so you don't want to eliminate it.
|
kaic
2013-10-15 11:32:28 |
The correct answer is (B)
|
poopdog
2016-04-09 23:52:41 |
This is wrong.
|
|  | johw
2009-09-23 20:40:40 | Is this solution correct?
We use the same solution as yosun for 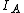
For 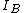 , we recall the original definition of moment of inertia, , we recall the original definition of moment of inertia,
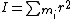 , ,
Hence,
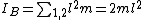
Thus, the ratio is just 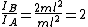 . . |  | sonnb
2008-05-29 19:45:36 | A more basic solution is as follows: The kinetic energy of the three particles moving about A with angular velocity 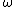 is is 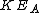 = = 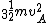 = = 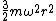 = = 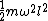 where where 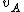 = =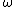 r and r = l/ r and r = l/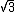 . .
The kinetic energy of the two particles moving about B with angular velocity 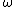 is is 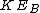 = = 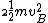 = m = m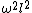 , since , since 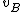 = =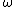 l. The ratio of these two kinetic energies is 2, answer (B). l. The ratio of these two kinetic energies is 2, answer (B).
Camoph
2010-03-30 17:05:53 |
How do you obtain r=l/\sqrt{3}??. r(cos30)=l/2??. I don't agree.
|
Camoph
2010-03-30 17:11:08 |
How do you obtain r=l/\sqrt{3}??. r(cos30)=l/2??. I don't agree.
|
|  | Richard
2007-09-26 00:13:07 | First, I want to say thanks to the creator of this site. It looks like it takes a lot of work, and it makes a great resource.
The symmetry of this problem makes it simple.
You know that the center of mass is in the center of the triangle and that it is equidistant from the three masses. Thus, 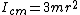 . .
Now, when you are at axis A, you can use the parallel axis theorem: 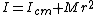 where M is the total mass of the system. In this case it is just where M is the total mass of the system. In this case it is just 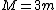 . .
Finally, because 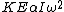 you take the ratio you take the ratio 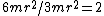 . .
flyboy621
2010-10-23 08:15:00 |
This is the best solution. You don't need to calculate r at all.
|
anum
2010-11-02 01:28:14 |
isn't A the center of mass?
|
anum
2010-11-02 01:31:31 |
oh got it! scratch the upper remark
|
anum
2010-11-02 01:31:57 |
oh got it! scratch the upper remark
|
|  | yipee
2007-09-15 17:39:34 | I think the solution here is completely wrong. For moment of inertia about A, Ia=3*(1/3)mr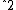 , where r is as shown in the above solution. So, then Ia=(1/3)ml , where r is as shown in the above solution. So, then Ia=(1/3)ml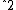 . Then, moment of inertia about B, Ib=0 + (1/3)ml . Then, moment of inertia about B, Ib=0 + (1/3)ml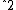 + (1/3)ml + (1/3)ml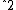 =(2/3)ml =(2/3)ml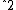 , where the zero comes from the mass at B. So, dividing the Kb by Ka then gives Ib/Ia = 2 as expected. , where the zero comes from the mass at B. So, dividing the Kb by Ka then gives Ib/Ia = 2 as expected.
Gaffer
2007-10-26 16:33:34 |
I was totally with you while taking the test. However, in looking back, I realized that we both made an improper assumption. We cannot assume that the moment of inertia for the particle at B is zero since it has extension. If the particles were the "very small" point particles we all love so much, that would be valid; since this problem is on the order of magnitude of the tangible, ie with dimensions, the particle at B will contribute to the net inertia.
Yosun's method is the safest mathematically.
|
errjones
2008-10-17 15:49:39 |
I think the issue here is that you're misunderstanding the parallel axis theorem, which is what I also did at first. Stated in Fowles, it goes
"The moment of inertia of a rigid body about any axis is equal to the moment of inertia about a parallel axis passing through the center of mass plus the product of the mass of the body and the square of the distance between the two axes."
So, the distance "d" in Yosun's solution is that distance between the two axes, namely A and B. The total mass would also still be 3m.
|
QuantumCat
2014-09-18 09:26:17 |
The moment of inertia between two masses is 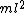 , and since there are two masses, , and since there are two masses, 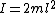
|
|  | ec2250
2007-09-07 20:13:34 | I don't understand why we need to add all three point masses in the parallel axis theorem. Doesn't the theorem only say we need to add the moment of inertia of the center of mass plus the mass and distance of the other axis? which would only be 1Md/(3)^.5? I'm pretty sure the solution is right, I just want a deeper explanation. Thanks. |  | jshariff
2007-04-12 17:25:07 | Correction to the LaTeX in the above correction =p
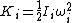 |  | nitin
2006-10-28 06:24:07 | The kinetic energy of rotation is $K_i=\frac{1}{2}I_i(\omega_i)^2 |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
